The dipole moment of compound AB is 10.92 D and that of compound CD is 12.45 D. The bond length AB is 2.72 Å and that of CD is 2.56 Å then for these compound true statement is
More ionic nature in AB
More ionic nature in CD
Equal in both
Not predicted
The correct Answer is:B
To determine the ionic nature of compounds AB and CD based on their dipole moments and bond lengths, we can calculate the percentage ionic character for each compound using the formula:
Percentage Ionic Character=(μe⋅d)×100
Where:
- μ = dipole moment in Coulomb-meters
- e = charge of an electron = 1.6×10−19 Coulombs
- d = bond length in meters
Step 1: Convert dipole moment from Debye to Coulomb-meters
1 Debye = 3.336×10−29 Coulomb-meters.
For compound AB:
μAB=10.92D=10.92×3.336×10−29C m=3.644×10−28C m
For compound CD:
μCD=12.45D=12.45×3.336×10−29C m=4.151×10−28C m
Step 2: Convert bond lengths from Ångstroms to meters
1 Ångstrom = 1×10−10 meters.
For compound AB:
dAB=2.72Å=2.72×10−10m
For compound CD:
dCD=2.56Å=2.56×10−10m
Step 3: Calculate the percentage ionic character for compound AB
Using the formula:
Percentage Ionic CharacterAB=(3.644×10−28(1.6×10−19)⋅(2.72×10−10))×100
Calculating the denominator:
(1.6×10−19)⋅(2.72×10−10)=4.352×10−29
Now substituting back:
Percentage Ionic CharacterAB=(3.644×10−284.352×10−29)×100≈83.8%
Step 4: Calculate the percentage ionic character for compound CD
Using the formula:
Percentage Ionic CharacterCD=(4.151×10−28(1.6×10−19)⋅(2.56×10−10))×100
Calculating the denominator:
(1.6×10−19)⋅(2.56×10−10)=4.096×10−29
Now substituting back:
Percentage Ionic CharacterCD=(4.151×10−284.096×10−29)×100≈101.3%
Conclusion
Since the percentage ionic character for compound CD is higher than that for compound AB, we conclude that compound CD has more ionic character.
Final Answer
The true statement is that compound CD has more ionic nature than compound AB.
- μ = dipole moment in Coulomb-meters
- e = charge of an electron = 1.6×10−19 Coulombs
- d = bond length in meters
1 Debye = 3.336×10−29 Coulomb-meters.
μAB=10.92D=10.92×3.336×10−29C m=3.644×10−28C m
μCD=12.45D=12.45×3.336×10−29C m=4.151×10−28C m
1 Ångstrom = 1×10−10 meters.
dAB=2.72Å=2.72×10−10m
dCD=2.56Å=2.56×10−10m
Using the formula:
Percentage Ionic CharacterAB=(3.644×10−28(1.6×10−19)⋅(2.72×10−10))×100
(1.6×10−19)⋅(2.72×10−10)=4.352×10−29
Percentage Ionic CharacterAB=(3.644×10−284.352×10−29)×100≈83.8%
Using the formula:
Percentage Ionic CharacterCD=(4.151×10−28(1.6×10−19)⋅(2.56×10−10))×100
(1.6×10−19)⋅(2.56×10−10)=4.096×10−29
Percentage Ionic CharacterCD=(4.151×10−284.096×10−29)×100≈101.3%
Since the percentage ionic character for compound CD is higher than that for compound AB, we conclude that compound CD has more ionic character.
The true statement is that compound CD has more ionic nature than compound AB.
Similar Questions
Dipole moment of
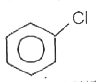 is 1.1 D hence dipole moment of given compound will be
is 1.1 D hence dipole moment of given compound will be
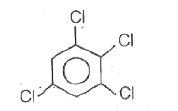
View SolutionIn [Pt(NH3)2Cl2], pt-Cl bond length is 2 Å and Cl-Cl distance is 2.88 Å then the compound is:
View SolutionCompare the dipole moments of the compounds in the following pairs.
CO2,SO2
View SolutionIf the dipole moment of AB molecule is given by 1.6 D and A - B the bond length is 1Å then % covalent character of the bond is
View SolutionThe observed dipole moment of HCl is 1.03D. If the bond length of HCL is 1.3Å, then the percent ionic character of H−Cl bond is
View SolutionThe observed dipole moment of HCl is 1.03D. If the bond length of HCL is 1.275Å, then the percent ionic character of H−Cl bond is
View SolutionThe observed dipole moment of HCl is 1.03 D. If the H-Cl bond length is 1.275 Å, calculate the per cent ionic character in HCI.
View SolutionIf the dipole moment of AB molecule is given by 1.2 D and A - B the bond length is 1Å then % ionic character of the bond is [Given : 1 debye =10−18 esu. Cm]
View SolutionIf the dipole moment of HCl is 1.08 D and the bond distance is 1.27Å, the partial charge on hydrogen and chlorine , respectively are
View SolutionThe bond length of H-X molecule is 1.2Å and the dipole moment of the molecule is 1.1D. Calculate % inonic character of the bond.
View Solution
