A seriesLCR circuit is connected to an ac voltage source. When L is removed from the circuit, the phase difference between current and voltage is π3. If instead C is removed from the circuit phase difference is again π3 between current and voltage. Power factor of circuit is:
zero
0.5
1
-1
To solve the problem, we need to analyze the series LCR circuit under two different conditions: when the inductor (L) is removed and when the capacitor (C) is removed. We will then find the power factor of the circuit.
1. Understanding the Circuit:
- We have a series LCR circuit connected to an AC voltage source.
- The components are: Resistance (R), Inductance (L), and Capacitance (C).
2. Case 1: Inductor (L) is Removed
- When L is removed, the circuit consists of only R and C.
- The phase difference (Φ) between the current and voltage is given as π3.
- The relationship for phase angle in an RC circuit is given by:
tan(Φ)=XCR
- Here, XC is the capacitive reactance, which can be expressed as:
XC=1ωC
- Substituting Φ=π3:
tan(π3)=√3=XCR
- Therefore, we have:
XC=R√3
3. Case 2: Capacitor (C) is Removed
- When C is removed, the circuit consists of only R and L.
- The phase difference (Φ) between the current and voltage is again given as π3.
- The relationship for phase angle in an RL circuit is given by:
tan(Φ)=XLR
- Where XL is the inductive reactance, expressed as:
XL=ωL
- Substituting Φ=π3:
tan(π3)=√3=XLR
- Therefore, we have:
XL=R√3
4. Finding the Power Factor of the LCR Circuit:
- The power factor (PF) of the LCR circuit is defined as:
PF=cos(Φ)
- The impedance Z of the LCR circuit is given by:
Z=√R2+(XL−XC)2
- Since XL=R√3 and XC=R√3:
XL−XC=R√3−R√3=0
- Therefore, the impedance simplifies to:
Z=√R2+02=R
- Now, substituting into the power factor formula:
PF=RZ=RR=1
Final Answer:
The power factor of the circuit is 1.
- We have a series LCR circuit connected to an AC voltage source.
- The components are: Resistance (R), Inductance (L), and Capacitance (C).
- When L is removed, the circuit consists of only R and C.
- The phase difference (Φ) between the current and voltage is given as π3.
- The relationship for phase angle in an RC circuit is given by:
tan(Φ)=XCR
- Here, XC is the capacitive reactance, which can be expressed as:
XC=1ωC
- Substituting Φ=π3:
tan(π3)=√3=XCR
- Therefore, we have:
XC=R√3
- When C is removed, the circuit consists of only R and L.
- The phase difference (Φ) between the current and voltage is again given as π3.
- The relationship for phase angle in an RL circuit is given by:
tan(Φ)=XLR
- Where XL is the inductive reactance, expressed as:
XL=ωL
- Substituting Φ=π3:
tan(π3)=√3=XLR
- Therefore, we have:
XL=R√3
- The power factor (PF) of the LCR circuit is defined as:
PF=cos(Φ)
- The impedance Z of the LCR circuit is given by:
Z=√R2+(XL−XC)2
- Since XL=R√3 and XC=R√3:
XL−XC=R√3−R√3=0
- Therefore, the impedance simplifies to:
Z=√R2+02=R
- Now, substituting into the power factor formula:
PF=RZ=RR=1
The power factor of the circuit is 1.
Similar Questions
In an electrical circuit R,L,C and an AC voltage source are all connected in series. When L is removed from the circuit, the phase difference between the voltage and the current in the circuit is π/3. If instead, C is removed from the circuit, difference the phase difference is again π/3. The power factor of the circuit is
View SolutionIn an electrical circuit R,L, C and a.c voltage source are all connected in series. When L is removed from the circuit , the phase difference between the voltage and current in the circuit is π/6. If instead ,C is removed from the circuit , the phase difference is again π/6 . The power factor of the circuit is
View Solution
Knowledge Check
In an electrical circuit R,L,C and an AC voltage source are all connected in series. When L is removed from the circuit, the phase difference between the voltage and the current in the circuit is π/3. If instead, C is removed from the circuit, difference the phase difference is again π/3. The power factor of the circuit is
A12B1√2C1D√32
An Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
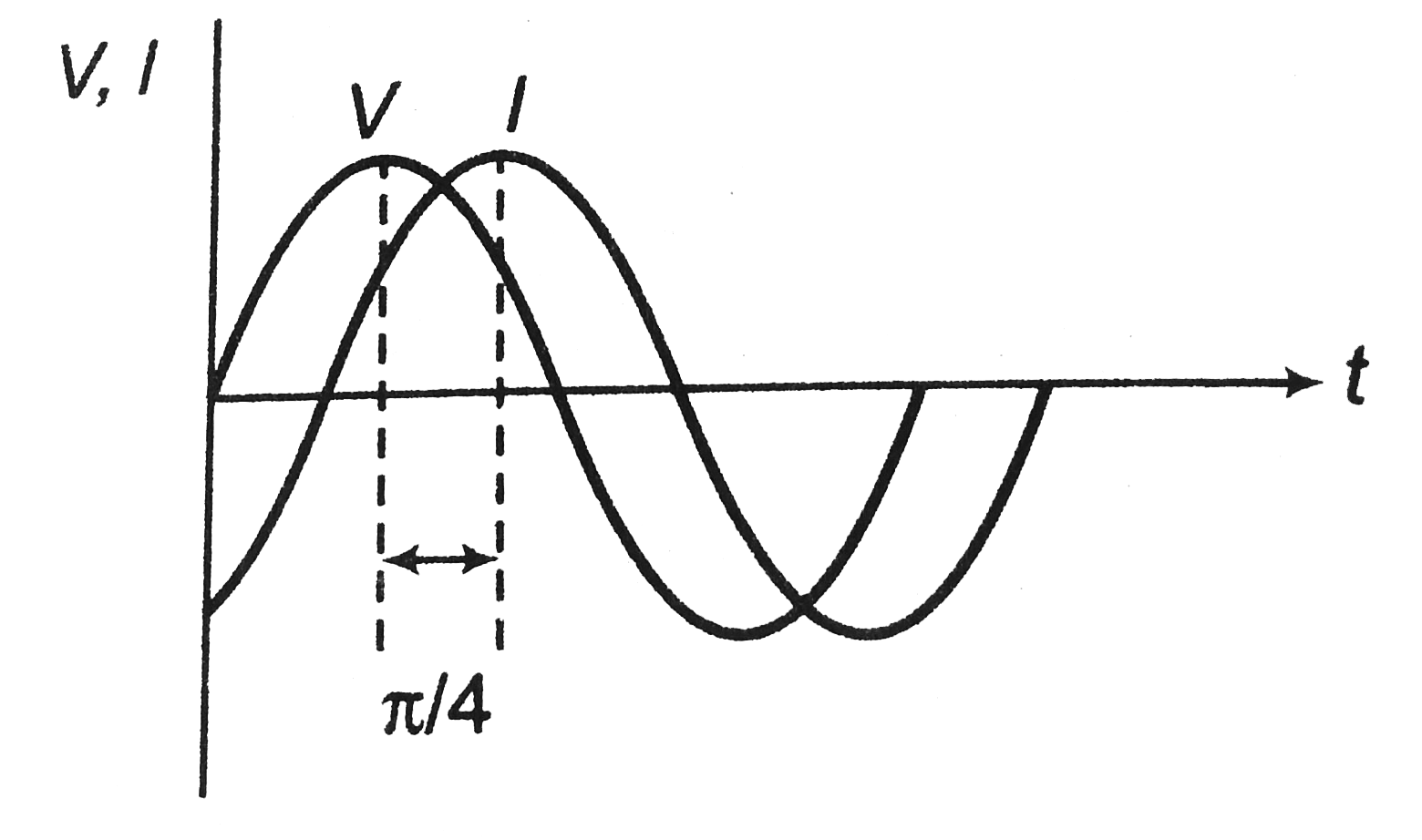 .
.
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View SolutionFor wattless power is an AC circuit, the phase angle between the current and voltagge is
View SolutionIn the shown AC circuit phase different between current I1 and I2 is
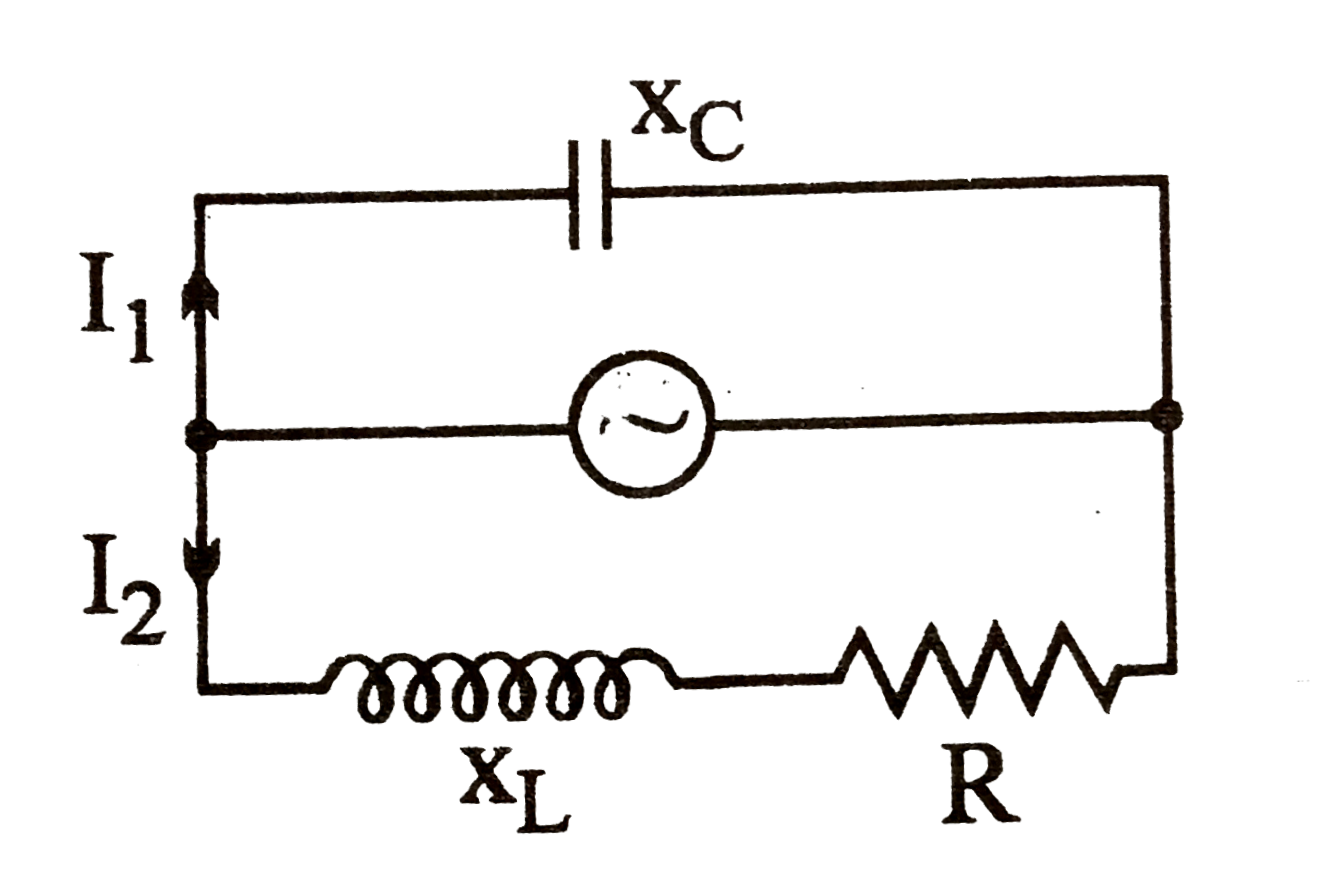
View SolutionThe phase angle between current and voltage in a purely inductive circuit is
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View SolutionFind the phase difference between voltage and current in L-C circuit.
View Solution
