Question

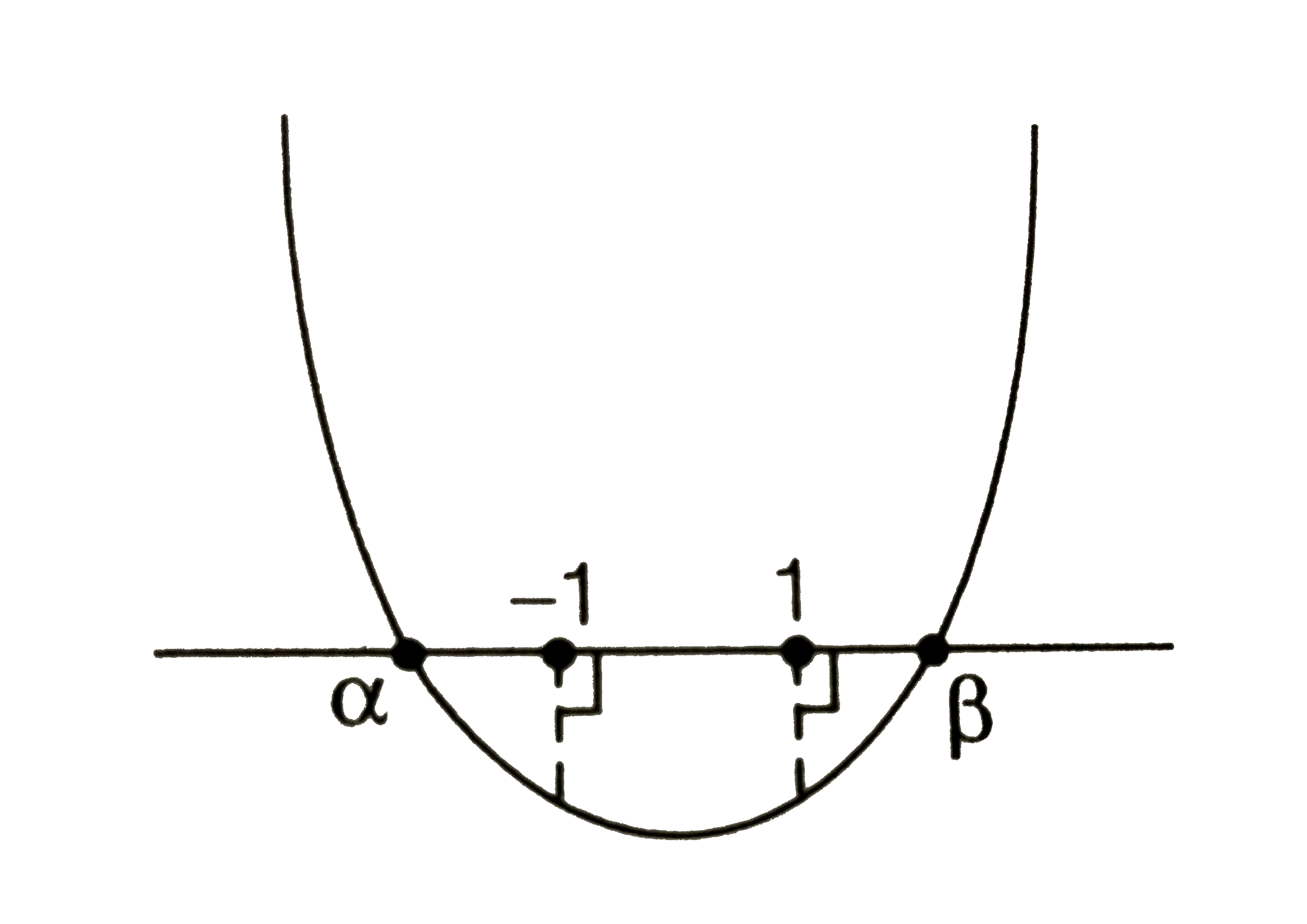
Let $a,b,c$
be real. If $a{x}^2+bx+c=0$
has two real roots $\alpha and\beta ,where\alpha ⟨-1and\beta ⟩-1$
, then show that $1+\frac{c}{a}+\left|\frac{b}{a}\right|<0$

Explanation

Since `alpha lt -1` and `betagt1`
`alpha+lamda=-1` and `beta=1+mu [ lamda, mugt0]`
Now `1+c/a+|b/a|=1+alpha beta+|alpha+beta|`
`=1+(-1-lamda)(1+mu)+|-1-lamda+1+mu|`
`=1-1-mu-1lamda-lamdamu+|mu-lamda|`
`=-mu-lamda-lamda mu+mu-lamda` [if `mugtlamda`]
and `=-mu-lamda-lamda mu+lamda-mu` [if `lamdagtmu`]
`:.1+c/a+|b/a|=-2lameda-lamda mu` or `-2mu-lamda mu`
On both cases `1+c/a+|b/a|lt0 [ :' lamda, mugt0]`
Aliter
`:'ax^(2)+bx+c=0, a!=0`
`x^(2)+b/ax+c/a=0`
Let `f(x)=x^(2)+b/ax+c/a`
`f(-1)lt0` and `f(1)lt0`
`implies1-b/a+c/alt0` and `1+b/a+c/alt0`
Then `1+|b/a|+c/alt0`