Question

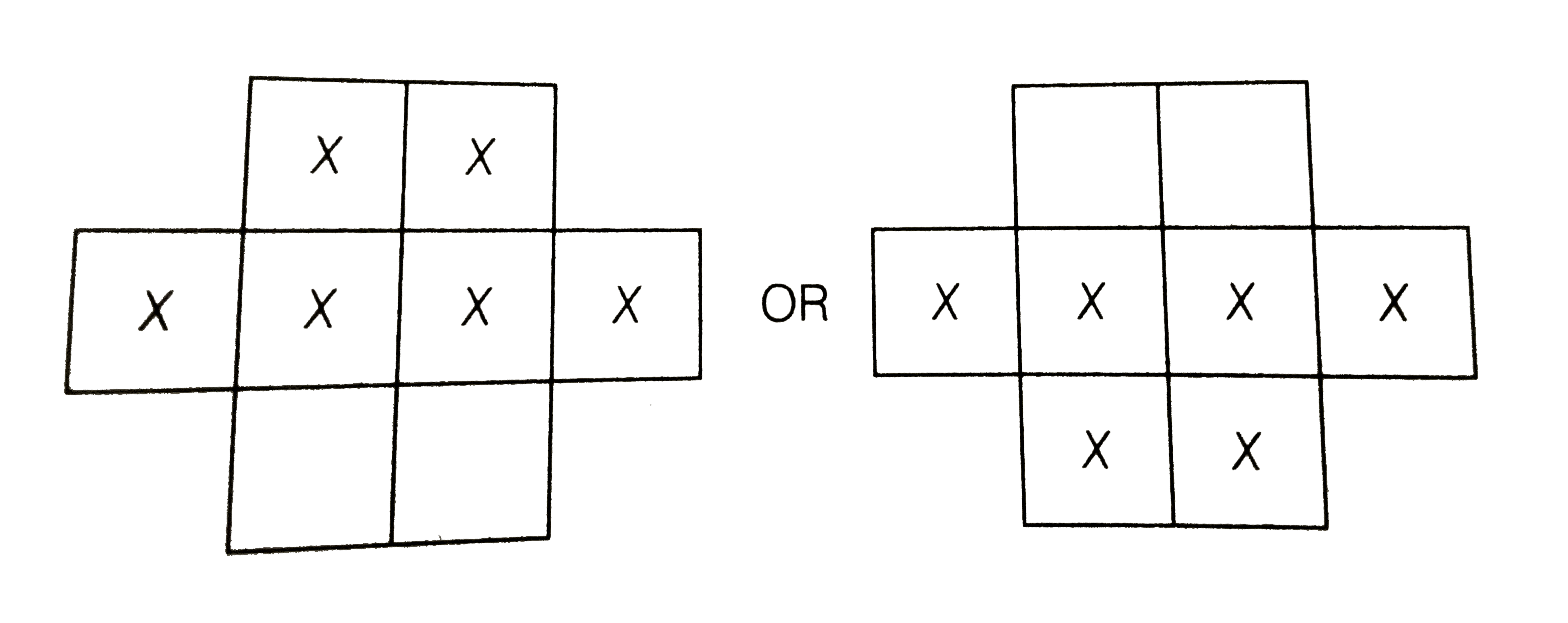
Six X 's have to be placed in the squares of the figure below, such that each row contains atleast one X. in how many different ways can this be done?

Explanation

In the given figure there are 8 squares and we have to place 6X's this can be donne in
`.^(8)C_(6)=.^(8)C_(2)=(8*7)/(1*2)=28` ways
But these include the possibility that either headed row or lowest row may not have any X. these two possibilities are to be excluded.
`therefore` Required number of ways=28-2=26