Question

If $\overrightarrow{a},\overrightarrow{b}$
are any two vectors, then give the geometrical
interpretation of relation $|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|$

Explanation

Let OA=a and AB=b. completing the parallelogram OABC.

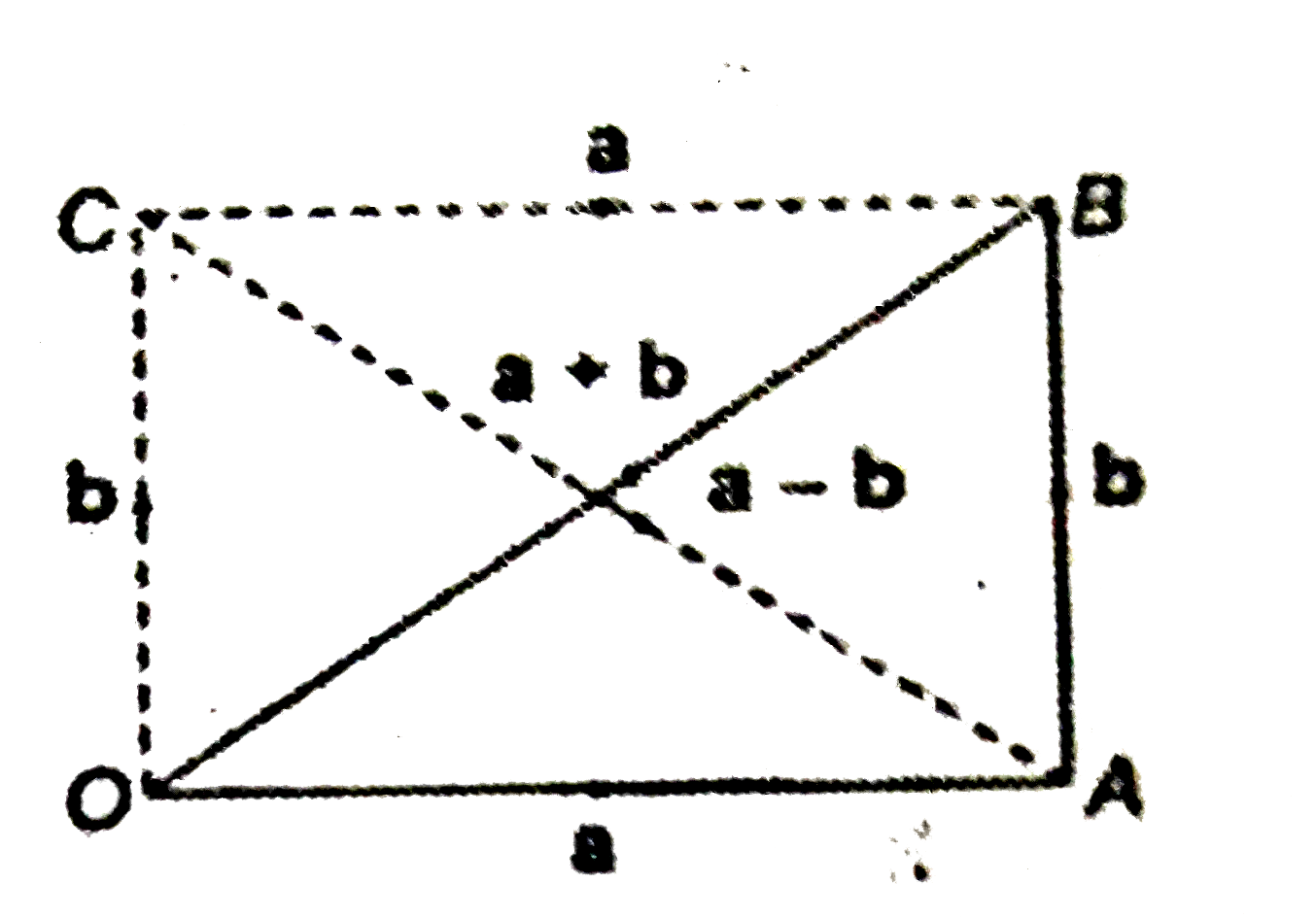
Then, OC=b and CB=a
from `DeltaOAB`, we have
`OA+AB=Obimpliesa+b=OB` . . . (i)
From `DeltaOCA,` we have
`OC+CA=OA`
`impliesb+CA=aimpliesCA=a-b` . . . (ii)
Clearly, `|a+b|=|a-b|implies |OB|=|CA|`
Diagonals of parallelogram OABC are qual.
OABC is a rectangle.
`implies OA bot OC implies a bot b`.