In a quadrilateral $P Q R S, \to P Q = \to a, \to Q R = \to b, \to S P = \to a - \to b, M$ is the midpoint of $\to Q R a n d X$ is a point on $S M$ such that $S X = \frac{4}{5} S M .$ Prove that $P, X a n d R$ are collinear.

A

$P X = \frac{1}{5} P R$

B

$P X = \frac{3}{5} P R$

C

$P X = \frac{2}{5} P R$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

If we take point P as the origin, the position vectors of Q and S are a and b-a respectively.
In $Δ P Q R$ , we have

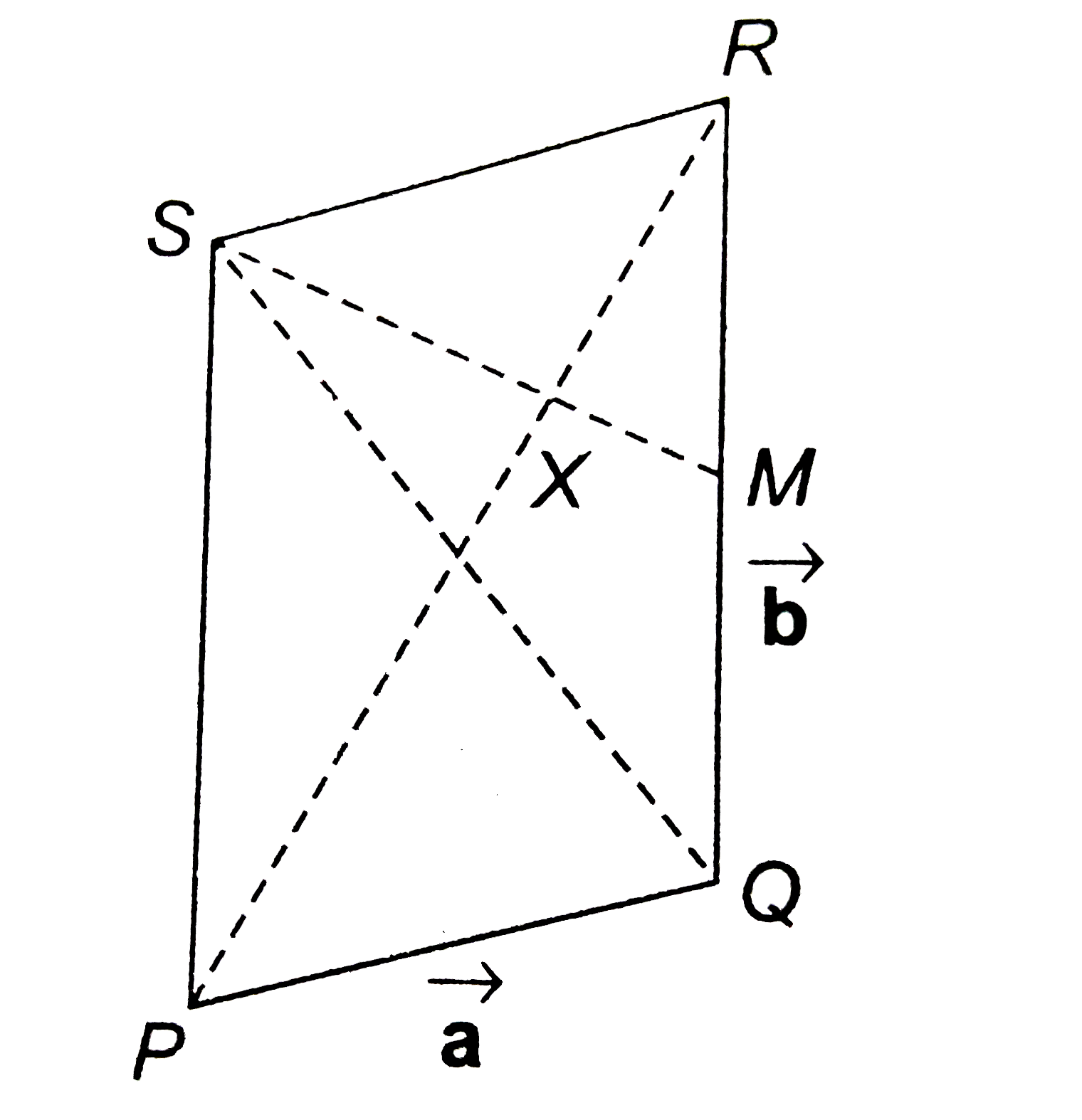
$P R = P Q + Q R \Rightarrow P R = a + b$
$∴$ Position vector of R=a+b
$\Rightarrow P V$ or $M = \frac{a + (a + b)}{2} = (a + \frac{1}{2} b)$
Now, $S X = \frac{4}{5} S M$
$\Rightarrow X M = S M - S X = S M - \frac{4}{5} S M = \frac{1}{5} S M$
$∴ S X : X M = 4 : 1$
$\Rightarrow P V$ of $X = \frac{4 (a + \frac{1}{2} b) + 1 (b - a)}{4 + 1}$
$= \frac{3 a + 2 b}{5} \Rightarrow P X = \frac{3}{5} (a + b)$
$\Rightarrow P X = \frac{3}{5} P R$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS ENGLISH-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile