If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
The correct Answer is:D
We know by fundamental theorem of proportionality that,

In triangle,
Hence, .
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions
1 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusIn a triangle ABC, AB=7cm,AC=5√2cm also ∠A=135∘ and point E and F are the mid points of side AB and AC respectively then what will be the length of EF?
AA) 12 cmBB) 14 cmCC) 13/2 cmDD) 16 cmIn the triangle given below, D and E are mid points of AF and AG respectively. F and G are mid points of AB and AC respectively. If DE = 2.4 cm. then BC is equal to:
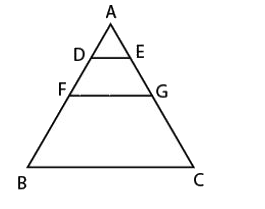 A4.8 cmB3.6 cmC9.6 cmD7.2 cm
A4.8 cmB3.6 cmC9.6 cmD7.2 cm
ABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionABC is a triangle in which D, E and F are the mid-points of the sides AC, BC and AB respectively. What is the ratio of the area of the shaded to the unshaded region in the triangle?

View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View SolutionIf D, E and F are respectively, the mid-points of AB, AC and BC in ΔABC, then BE + AF is equal to
View Solution
