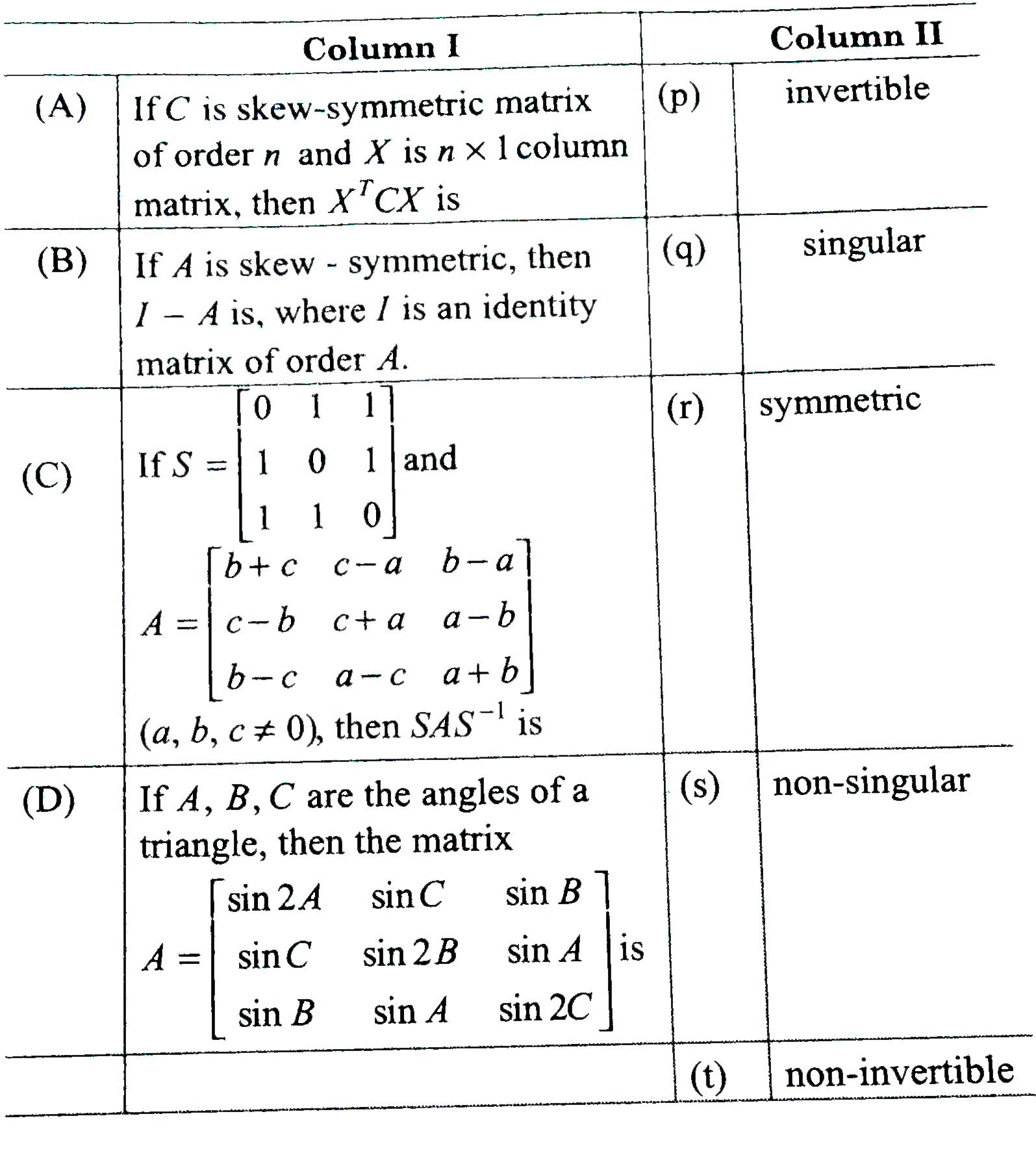The correct Answer is:(A)→(q,t);(B)→(p,s);(C)→(p,r,s);(D)→(q,r,t)
(A)→(q,t),(B)→(p,s),(C)→(p,r,s),(D)→(q,r,t)
(A) Here, X is a nn×1 matrix, C is n×n matrix andf XT is a
1×n matrix.
Let XTCX=[λ], then (XTCX)T=XTCT(XT)T=XT(−C)X=−XTCX
∴[λ]=−[λ]
⇒λ=0
⇒XTCX=O
(B) Consider the homogeneous sytemm
(I−A)X=O
⇒AX=IX=X ...(i)
Now, (AX)T=XTAT⇒XT=−XTA
⇒XTX=−XTAX=−XTX
[from Eq. (i) ]
⇒2XTX=O⇒|X|=O
(I−A)X=O has only trivial solution
∴I−A is non- singular
⇒(I−A) is invertible
(C) ∵S=⎡⎢⎣011101110⎤⎥⎦
⇒S−1=12⎡⎢⎣−1111−1111−1⎤⎥⎦
We have SA=⎡⎢⎣011101110⎤⎥⎦⎡⎢⎣b+cc−ab−ac−bc+aa−bb−ca−ca+b⎤⎥⎦
=⎡⎢⎣02a2a2b02b2c2c0⎤⎥⎦
∴SAS−1=⎡⎢⎣02a2a2b02b2c2c0⎤⎥⎦12⎡⎢⎣−1111−1111−1⎤⎥⎦
=⎡⎢⎣0aab0bcc0⎤⎥⎦⎡⎢⎣−1111−1111−1⎤⎥⎦⎡⎢⎣2a000ab000ac⎤⎥⎦
∣∣SAS−1∣∣=8abc≠0
∵A=⎡⎢⎣sin2AsinCsinBsinCsin2BsinAsinBsinAsin2C⎤⎥⎦
|A|=⎡⎢⎣2akcosAckbkck2bkcosBakbkak2ckcosC⎤⎥⎦
=k3⎡⎢⎣acosA+acosAacosB+bcosAacosC+cosAacosB+bcosAbcosB+bcosBbcosC+ccosBacosC+ccosAbcosC+ccosBccosC+ccosC⎤⎥⎦
=k3∣∣
∣∣acosA0bcosB0ccosC0∣∣
∣∣×∣∣
∣∣cosAa0cosBb0cosCc0∣∣
∣∣=k3⋅0⋅0=0
Topper's Solved these Questions
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Statement I And Ii Type Questions)
10 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Subjective Type Questions)
14 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
29 Videos
Similar Questions
(Statement1 Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement - 1 If matrix A=[aij]3×3,B=[bij]3×3, where aij+aji=0andbij−bji=0 then A4B5 is non-singular
matrix.
Statement-2 If A is non-singular matrix, then |A|≠0.
View SolutionIf S is a real skew-symmetric matrix, then prove that I−S is non-singular and the matrix A=(I+S)(I−S)−1 is orthogonal.
View SolutionLet A,B,C,D be (not necessarily ) real matrices such that AT=BCD,BT=CDA,CT=DABandDT=ABC for the matrix S=ABCD the least value of k such that Sk=S is
View SolutionStatement-1: For every natural number n≥2,
1√1+1√2+1√3+...+1√n>√n
Statement-2: For every natural number n≥2,
√n(n+1)<n+1
View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution