If α,β,γ be the angles which a line makes with the coordinates axes, then
A. cos(2α)+cos(2β)+cos(2γ)−1=0
B. cos(2α)+cos(2β)+cos(2γ)−2=0
C. cos(2α)+cos(2β)+cos(2γ)+1=0
D. cos(2α)+cos(2β)+cos(2γ)+2=0
The correct Answer is:(c)
To solve the problem, we need to analyze the relationship between the angles α, β, and γ that a line makes with the coordinate axes and how they relate to the cosine of those angles.
1. Understanding the Angles:
- Let α, β, and γ be the angles that a line makes with the x-axis, y-axis, and z-axis, respectively.
2. Using the Property of Cosines:
- A fundamental property in three-dimensional geometry states that for any line in space, the sum of the squares of the cosines of the angles it makes with the coordinate axes is equal to 1:
cos2α+cos2β+cos2γ=1
3. Manipulating the Equation:
- We can manipulate this equation by multiplying both sides by 2:
2(cos2α+cos2β+cos2γ)=2
- This simplifies to:
2cos2α+2cos2β+2cos2γ=2
4. Rewriting Each Term:
- We can express 2cos2θ in terms of 1+cos2θ:
2cos2α=1+cos2α
2cos2β=1+cos2β
2cos2γ=1+cos2γ
5. Substituting Back:
- Substituting these back into our equation gives:
(1+cos2α)+(1+cos2β)+(1+cos2γ)=2
- This simplifies to:
3+cos2α+cos2β+cos2γ=2
6. Rearranging the Equation:
- Rearranging this equation leads to:
cos2α+cos2β+cos2γ=2−3
- Thus:
cos2α+cos2β+cos2γ+1=0
7. Conclusion:
- Therefore, we find that:
cos2α+cos2β+cos2γ+1=0
- This corresponds to option C in the question.
Final Answer:
The correct option is:
cos2α+cos2β+cos2γ+1=0
- Let α, β, and γ be the angles that a line makes with the x-axis, y-axis, and z-axis, respectively.
- A fundamental property in three-dimensional geometry states that for any line in space, the sum of the squares of the cosines of the angles it makes with the coordinate axes is equal to 1:
cos2α+cos2β+cos2γ=1
- We can manipulate this equation by multiplying both sides by 2:
2(cos2α+cos2β+cos2γ)=2
- This simplifies to:
2cos2α+2cos2β+2cos2γ=2
- We can express 2cos2θ in terms of 1+cos2θ:
2cos2α=1+cos2α
2cos2β=1+cos2β
2cos2γ=1+cos2γ
- Substituting these back into our equation gives:
(1+cos2α)+(1+cos2β)+(1+cos2γ)=2
- This simplifies to:
3+cos2α+cos2β+cos2γ=2
- Rearranging this equation leads to:
cos2α+cos2β+cos2γ=2−3
- Thus:
cos2α+cos2β+cos2γ+1=0
- Therefore, we find that:
cos2α+cos2β+cos2γ+1=0
- This corresponds to option C in the question.
The correct option is:
cos2α+cos2β+cos2γ+1=0
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - JEE Type Solved Examples : Matching Type Questions
4 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise For Session 1
12 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
If α,β,γ are the angles which a line makes with the coordinate axes ,then (A) sin2α=cos2β+cos2γ (B) cos2α+cos2β+cos2γ=2 (C) cos2α+cos2β+cos2γ=1 (D) sin2α+sin2β=1+cos2γ
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
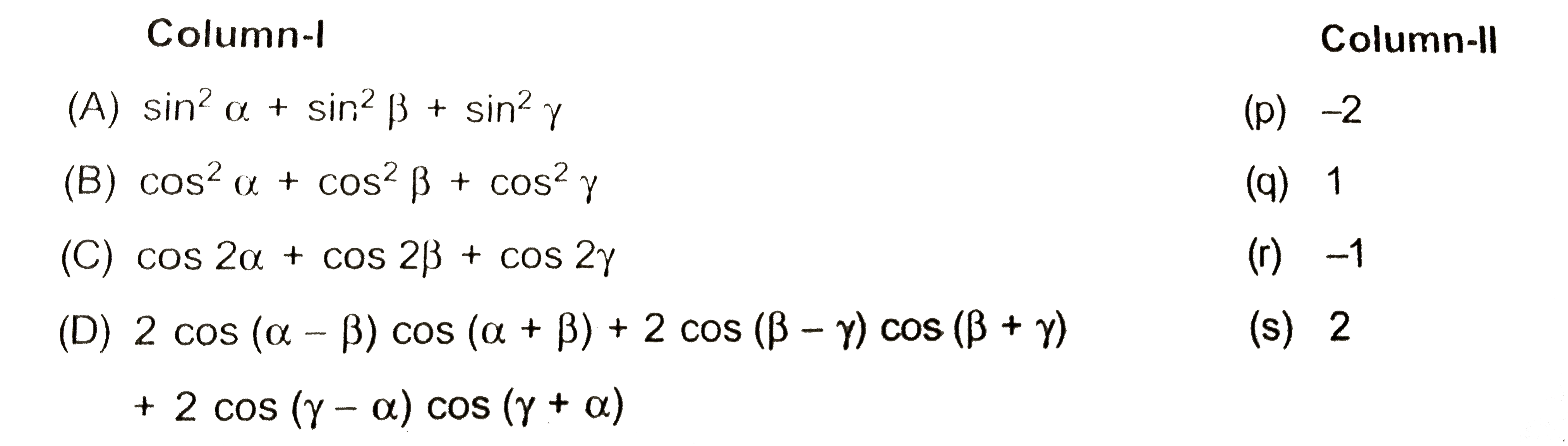
View Solution
Knowledge Check
If a line makes angles α,β,γ when the positive direction of coordinates axes, then write the value of sin2α+sin2β+sin2γ.
A3B2C1D4
If α,β,γ are the angle which a half ray makes with the positive direction of the axes then sin2α+sin2β+sin2γ=
(A) 1
(B) 2
(C) 0
(D) -1
View SolutionIf α,β,andγ are the an gles which a directed line makes with the positive directions of the co-ordinates axes, then find the value of sin2α+sin2β+sin2γ.
View SolutionIf α,β,andγ are the an gles which a directed line makes with the positive directions of the co-ordinates axes, then find the value of sin2α+sin2β+sin2γ.
View Solutionα2,β2,γ2 are the angle which a line makes with positive x,y,z axes respectively. What is the value of cosα+cosβ+cosγ? (A) 1 (B) −1 (C) 2 (D) 3
View SolutionIf α,β,γ be the eccentric angles of three points of an ellipse, the normals at which are concurrent, show that sin(α+β)+sin(β+γ)+sin(γ+α)=0.
View SolutionIf a line makes angle alpha,beta\ and\ gamma with the coordinate axes, find the value of cos2alpha+cos2beta+cos2gamma.
View SolutionIf a line makes anles α,β,γ with the coordinate axes, porve that sin2α+sin2β+sin2γ=2
View Solution
