ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.Ar(△ABD)=k2,ar(△BCD)=k3 then ar(△ACD) is
√k21+k22+k23
√k1k2k3k21+k22+k23
√∣∣(k21+k22−k23)∣∣
√∣∣(k21−k22−k23)∣∣
The correct Answer is:(c)
Step by step video & image solution for ABCD is a tetrahedron such that each of the triangleABC, triangleABD and triangleACD has a right angle at A. If ar(triangleABC) = k_(1). Ar(triangleABD)= k_(2), ar(triangleBCD)=k_(3) then ar(triangleACD) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (More Than One Correct Option Type Questions)
28 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise For Session 4
7 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
In △ABC, if Rr≤2, and a=2, then △ is equal to (△=ar(△ABC)).
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn △ABC, if ar (△ABC)=8. Then, a2sin(2B)+b2sin(2A) is equal to
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn △ABC, if √3sinC=2secA−tanA, then prove that triangle is right angled.
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
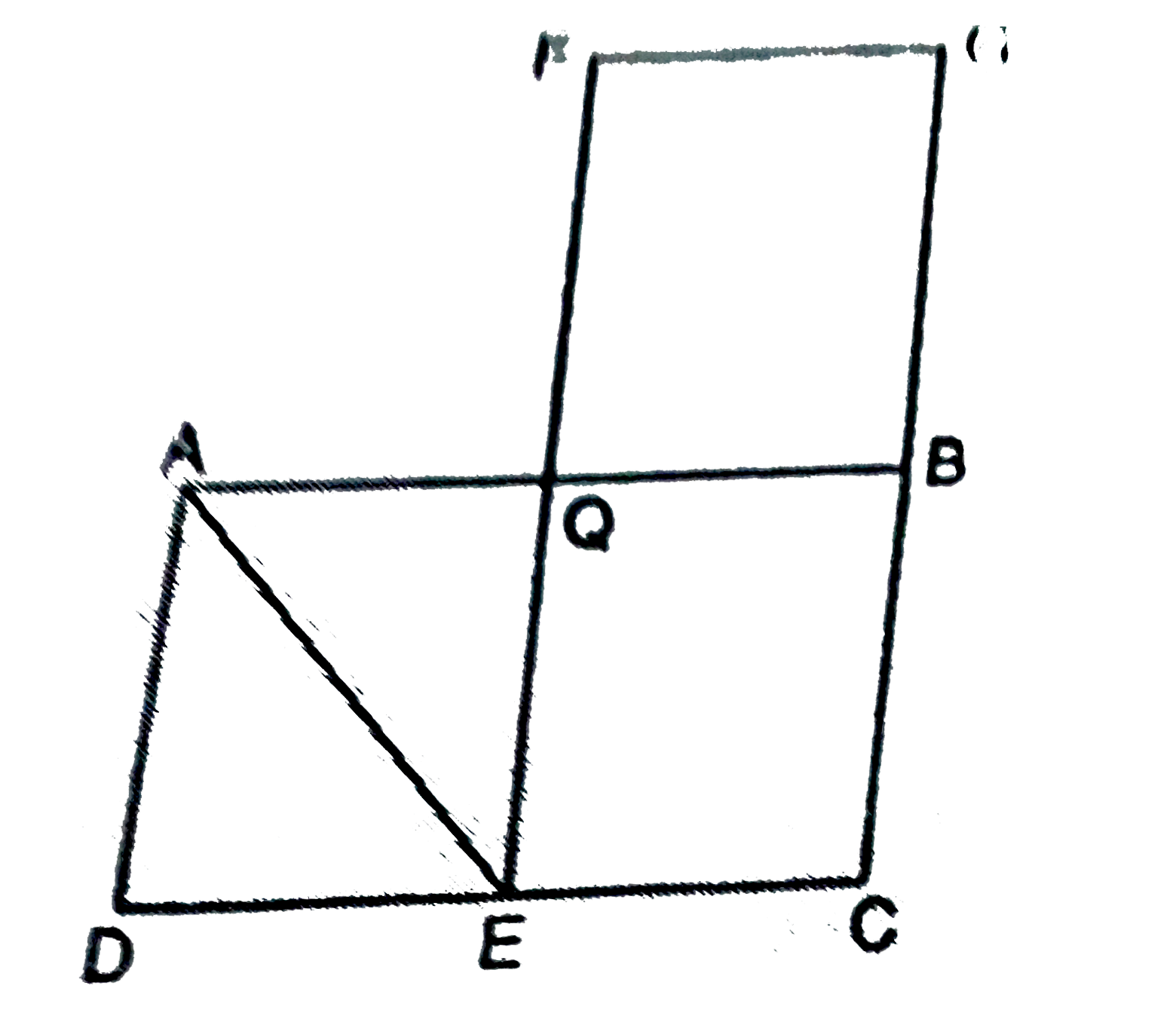
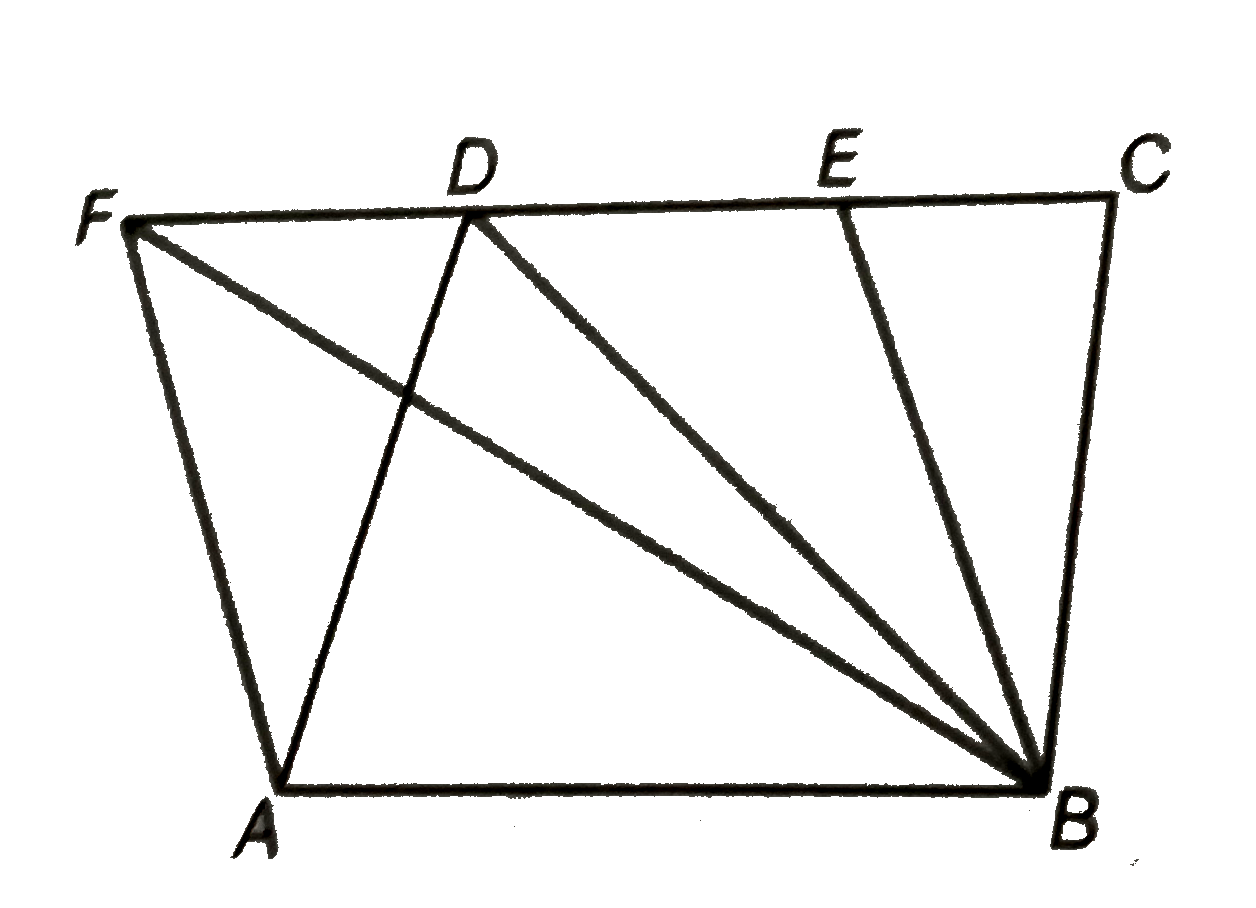
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
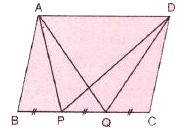
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View Solution
