What is vector equation of the line
The correct Answer is:(c)
To find the vector equation of a line in three-dimensional space, we can follow these steps:
1. Identify the Points:
- Let a be the position vector of a point on the line. This point can be represented as (x0,y0,z0) in Cartesian coordinates. Thus, a=x0i+y0j+z0k.
2. Determine the Direction Vector:
- Let b be the direction vector of the line. This vector indicates the direction in which the line extends. If the direction vector is given by (a,b,c), then b=ai+bj+ck.
3. Construct the Vector Equation:
- The vector equation of the line can be expressed as:
r=a+λb
- Here, r is the position vector of any point on the line, λ is a scalar parameter that varies along the line, a is the position vector of a specific point on the line, and b is the direction vector.
4. Interpret the Equation:
- As λ takes on different values, r traces out all points on the line. When λ=0, r equals a, which is a point on the line. As λ increases or decreases, r moves along the line in the direction of b.
Final Answer:
The vector equation of the line is given by:
r=a+λb
- Let a be the position vector of a point on the line. This point can be represented as (x0,y0,z0) in Cartesian coordinates. Thus, a=x0i+y0j+z0k.
- Let b be the direction vector of the line. This vector indicates the direction in which the line extends. If the direction vector is given by (a,b,c), then b=ai+bj+ck.
- The vector equation of the line can be expressed as:
r=a+λb
- Here, r is the position vector of any point on the line, λ is a scalar parameter that varies along the line, a is the position vector of a specific point on the line, and b is the direction vector.
- As λ takes on different values, r traces out all points on the line. When λ=0, r equals a, which is a point on the line. As λ increases or decreases, r moves along the line in the direction of b.
The vector equation of the line is given by:
r=a+λb
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 9 : Match Type Questions
7 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Single Integer Answer Type Questions)
26 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
Knowledge Check
What is the equation of the line that pases through the points (−3,1)and(1,3) ?
Ay=−x+2By=−x−2Cy=x−2Dy=x+2
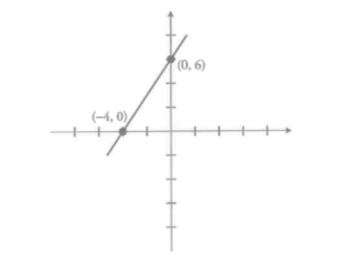
What is the equation of the line shown?
View SolutionWrite the vector equation of the line passing the point (5,2,-4) and parallel to the vector 3ˆi+2ˆj−8ˆk
View SolutionWrite the vector equation of the line given by x−53=y+47=z−62
View SolutionThe Cartesian equations of a line are 6x+2=3y−1=3z−2. Find its direction ratios and also find a vector equation of the line.
View SolutionThe Cartesian equations of a line are 6x−2=3y+1=2z−2. Find its direction ratios and also find a vector equation of the line.
View SolutionThe Cartesian equations of a line are 6x−2=3y+1=2z−2. Find its direction ratios and also find a vector equation of the line.
View SolutionThe Cartesian equations of a line are 6x−2=3y+1=2z−2. Find its direction ratios and also find vector equation of the line.
View Solution