Show that the area of the triangle with vertices (λ,λ−2),(λ+3,λ) and (λ+2,λ+2) is independent of λ.
To find the area of the triangle with vertices at the points A(λ,λ−2), B(λ+3,λ), and C(λ+2,λ+2), we can use the formula for the area of a triangle given by the coordinates of its vertices:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Step 1: Assign the coordinates
Let:
- A(x1,y1)=(λ,λ−2)
- B(x2,y2)=(λ+3,λ)
- C(x3,y3)=(λ+2,λ+2)
Step 2: Substitute the coordinates into the area formula
Substituting the coordinates into the area formula:
Area=12|λ(λ−λ−2)+(λ+3)(λ+2−(λ−2))+(λ+2)((λ−2)−λ)|
Step 3: Simplify the expression
Calculating each term:
1. The first term:
λ(λ−λ−2)=λ(−2)=−2λ
2. The second term:
(λ+3)(λ+2−λ+2)=(λ+3)(4)=4λ+12
3. The third term:
(λ+2)((λ−2)−λ)=(λ+2)(−2)=−2λ−4
Combining these:
Area=12|−2λ+4λ+12−2λ−4|
Step 4: Combine like terms
Simplifying the expression inside the absolute value:
−2λ+4λ−2λ+12−4=0λ+8=8
Step 5: Calculate the area
Thus, we have:
Area=12|8|=82=4
Conclusion
The area of the triangle is 4, which is independent of λ.
Let:
- A(x1,y1)=(λ,λ−2)
- B(x2,y2)=(λ+3,λ)
- C(x3,y3)=(λ+2,λ+2)
Substituting the coordinates into the area formula:
Calculating each term:
1. The first term:
λ(λ−λ−2)=λ(−2)=−2λ
2. The second term:
(λ+3)(λ+2−λ+2)=(λ+3)(4)=4λ+12
(λ+2)((λ−2)−λ)=(λ+2)(−2)=−2λ−4
Area=12|−2λ+4λ+12−2λ−4|
Simplifying the expression inside the absolute value:
−2λ+4λ−2λ+12−4=0λ+8=8
Thus, we have:
Area=12|8|=82=4
The area of the triangle is 4, which is independent of λ.
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 4
17 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Option Correct Type Questions)
15 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If the points A(λ,2λ),B(3λ,3λ)andC(3,1) are collinear, then λ=
View SolutionTransition between three energy energy levels in a particular atom give rise to three Spectral line of wevelength , in increasing magnitudes. λ1,λ2 and λ3. Which one of the following equations correctly ralates λ1,λ2 and λ3?
λ1=λ2−λ3
λ1=λ3−λ2
1λ1=1λ2+1λ3
1λ2=1λ3+1λ1
View SolutionLet αandβ be the values of x obtained form the equation λ2(x2−x)+2λx+3=0andifλ1,λ2 be the two values of λ for which αandβ are connected by the relation αβ+βα=43 . then find the value of λ21λ2+λ22λ1andλ21λ22+λ22λ21
View SolutionIf →a satisfies →a×(ˆi+2ˆj+ˆk)=ˆi−ˆk, then →a is equal to a.λˆi+(2λ−1)ˆj+λˆk,λ∈R b. λˆi+(1−2λ)ˆj+λˆk,λ∈R c. λˆi+(2λ+1)ˆj+λˆk,λ∈R d. λˆi−(1+2λ)ˆj+λˆk,λ∈R
View SolutionIf the circumcentre of the triangle whose vertices are (3,2,−5), (−3,8,−5) and (−3,2,1) is (−1,λ,−3) the integer λ must be equal to……
View Solution10 different vectors are lying on a plane out of which four are parallel with respect to each other. Probability that three vectors chosen from them will satisfy the equation λ1a+λ2b+λ3c=0, where λ1,λ2andλ3≠=0 is
View SolutionIf the direction ratios of two lines are (1,λ,2)and(λ,λ+1,λ) and the angle between the lines is 90∘ then
the modulus of sum of all values of λ is ________
View SolutionThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
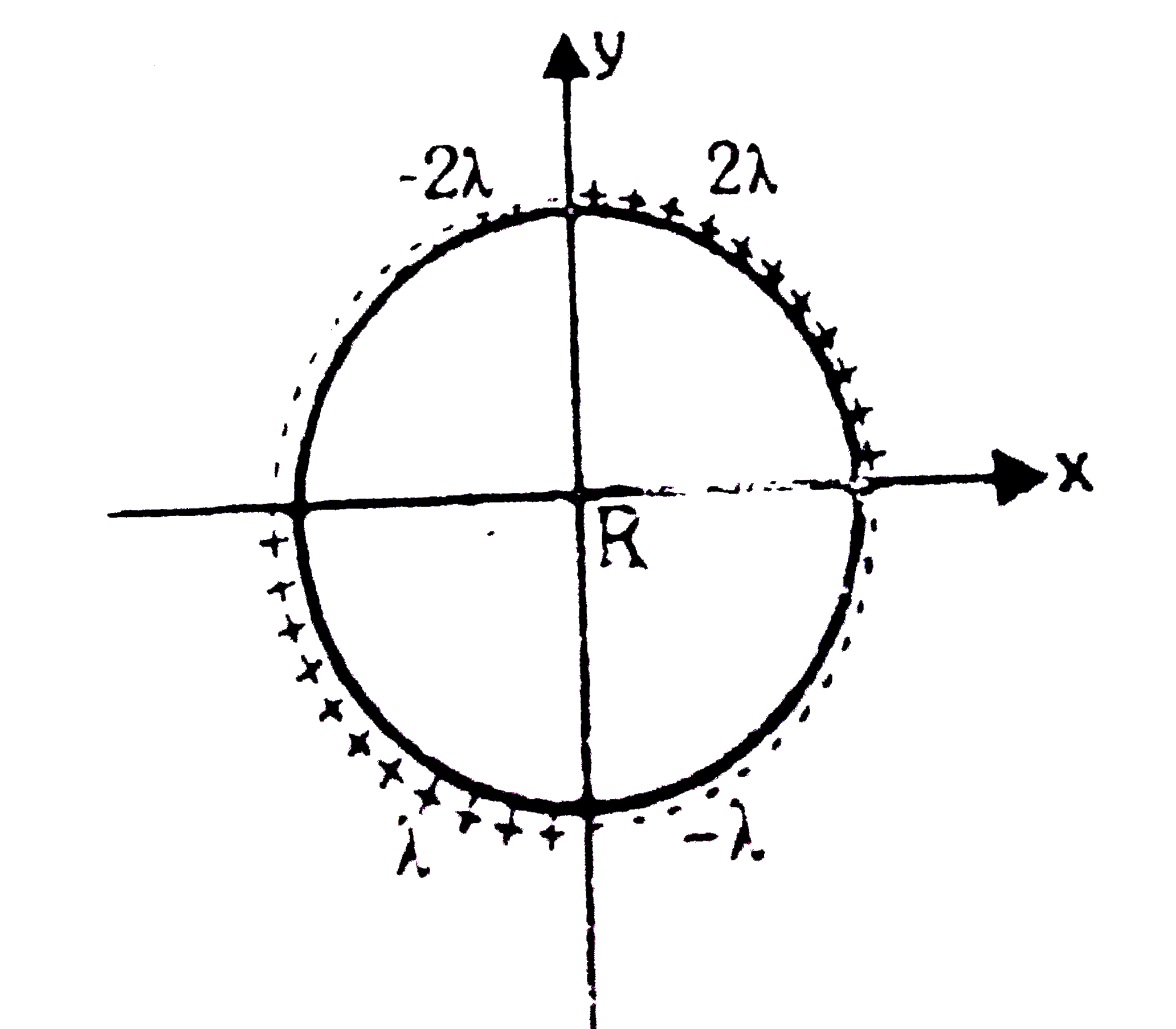
View SolutionA certain radioactive material can undergo three constant λ,2λ and 3λ. Then, the effective decay constant λeff is equal to nλ. What is the value of n?
View SolutionA variable plane moves so that the sum of reciprocals of its intercepts on the three coordinate axes is constant λ . It passes through a fixed point whose coordinate are (a) (λ,λ,λ) (b) (−1λ,−1λ,−1λ) (c) (1λ,1λ,1λ) (d) (−λ,−λ,−λ).
View Solution
