The vertices of a triangle are A(−10,8),B(14,8) and C(−10,26). Let G, I, H, O be the centroid, incentre, orthocentre, circumcentre respectively of ΔABC.
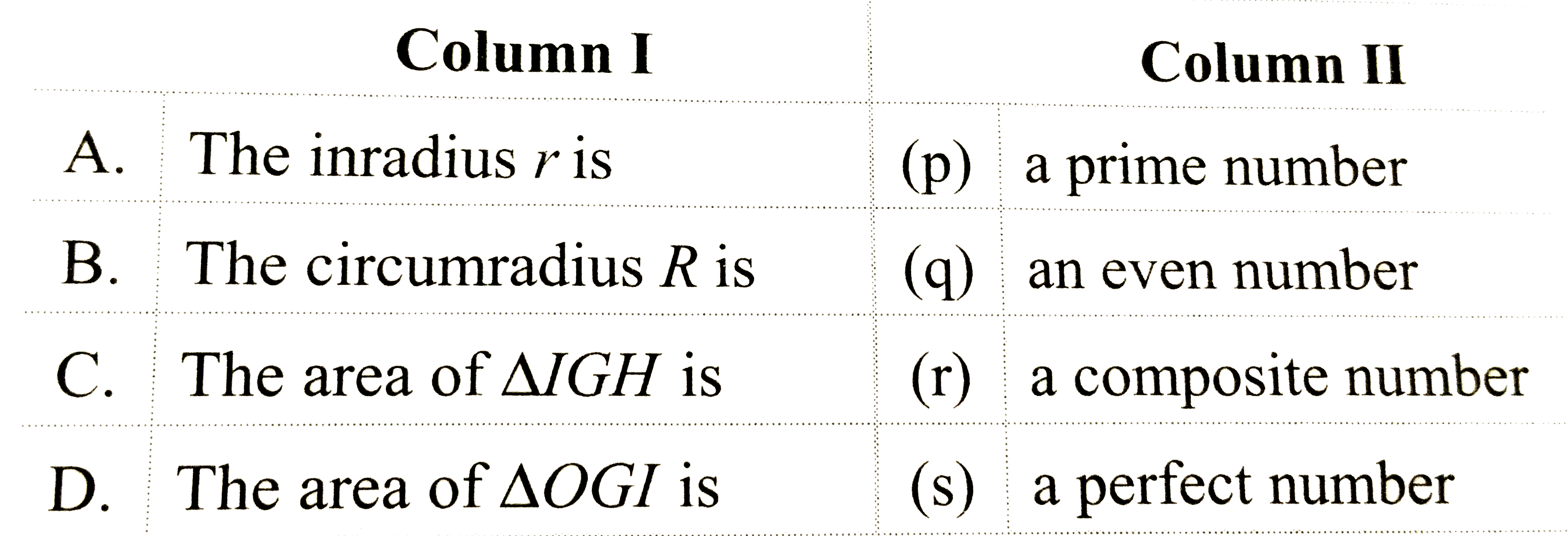
The correct Answer is:(A)→(q,r,s);(B)→(r);(C)→(q,r,s);(D)→(p)
Step by step video & image solution for The vertices of a triangle are A(-10, 8), B(14,8) and C(-10, 26). Let G, I, H, O be the centroid, incentre, orthocentre, circumcentre respectively of Delta ABC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Statement I And Ii Type Questions)
4 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - EXERCISE : 7
4 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Integer Answer Type Questions)
5 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If the vertices of a triangle are at O(0,0),A(a,0)andB(0,b). Then, the distance between its circumcentre and orthocentre is
View SolutionIf the vertices of a triangle are at O(0,0),A(a,0)andB(0,a). Then, the distance between its circumcentre and orthocentre is
View SolutionThe vertices of a triangle are the points P(−26,17),Q(30,17)andR(10,2). If G and I be the centroid and incentre of the triangle PQR, then the value of (GI)2 is equal to
View SolutionThe vertices of a triangle an A(1,2),B(−1,3) and C(3, 4). Let D, E, F divide BC, CA, AB respectively in the same ratio.
Statement I : The centroid of triangle DEF is (1, 3).
Statement II : The triangle ABC and DEF have the same centroid.
View SolutionThe incentre of the triangle whose vertices are (-36, 7), (20, 7) and (0, -8) is
View SolutionFind the centroid of the triangle whose vertices are A(-1,0), B(5, -2) and C(8, 2).
View SolutionIf the orthocentre and centroid of a triangle are (-3, 5, 1) and (3, 3, -1) respectively, then its circumcentre is
View SolutionIf two vertices of a triangle are (−2,3) and (5,−1) the orthocentre lies at the origin, and the centroid on the line x+y=7 , then the third vertex lies at (a)(7,4) (b) (8,14)(c) (12 ,21) (d) none of these
View SolutionConsider the triangle whose vertices are (0,0),(5,12) and (16,12) Find coordinates of (i) Centroid (ii) Incentre (iii) Circumcentre
View SolutionIf the coordinates of orthocentre O' are centroid G of a ΔABC are (0,1) and (2,3) respectively, then the coordinates of the circumcentre are
View Solution
