The moment when A is at (1,2)andBisat(0,0). The derivative dxBdxA, is
16
8
9
2
To solve the problem of finding the derivative dxBdxA when point A is at (1, 2) and point B is at (0, 0), we can follow these steps:
1. Identify the Points:
- Point A is given as A(1,2).
- Point B is given as B(0,0).
2. Set Up the Derivative:
- We want to find the derivative dxBdxA. This represents how the x-coordinate of point B changes with respect to the x-coordinate of point A.
3. Use the Formula for the Slope:
- The slope (or derivative) between two points can be calculated using the formula:
slope=y2−y1x2−x1
- Here, we can consider point A as (x1,y1)=(1,2) and point B as (x2,y2)=(0,0).
4. Calculate the Differences:
- For the y-coordinates:
y2−y1=0−2=−2
- For the x-coordinates:
x2−x1=0−1=−1
5. Substitute into the Slope Formula:
- Now substituting these values into the slope formula:
dyBdxA=0−20−1=−2−1=2
6. Conclusion:
- Therefore, the derivative dxBdxA is equal to 2.
Final Answer:
dxBdxA=2
- Point A is given as A(1,2).
- Point B is given as B(0,0).
- We want to find the derivative dxBdxA. This represents how the x-coordinate of point B changes with respect to the x-coordinate of point A.
- The slope (or derivative) between two points can be calculated using the formula:
slope=y2−y1x2−x1
- Here, we can consider point A as (x1,y1)=(1,2) and point B as (x2,y2)=(0,0).
- For the y-coordinates:
y2−y1=0−2=−2
- For the x-coordinates:
x2−x1=0−1=−1
- Now substituting these values into the slope formula:
dyBdxA=0−20−1=−2−1=2
- Therefore, the derivative dxBdxA is equal to 2.
dxBdxA=2
Topper's Solved these Questions
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - EXAMPLE
3 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - SOLVED EXAMPLES
7 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
26 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
The moment when A is at (0,0) and B is at (1,2). The derivative dydx of line AB is
View SolutionLet f(x) be function defined on [0,1] such that f(1)=0 and for any a∈(0,1],∫a0f(x)dx−∫1af(x)dx=2f(a)+3a+b where b is constant.
b=
View SolutionLet f(x) be function defined on [0,1] such that f(1)=0 and for any a∈(0,1],∫a0f(x)dx−∫1af(x)dx=2f(a)+3a+b where b is constant.
The length of the subtangent of the curve y=f(x)atx=1/2 is:
View SolutionLet a>0andf(x) is monotonic increase such that f(0)=0andf(a)=b,then ∫a0f(x)dx+∫b0f−1(x)dx is equal to
View Solution∫L0dxax+b =
View SolutionThe value of ∫π20dx1+tan3x is (a) 0 (b) 1 (c) π2 (d) π
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
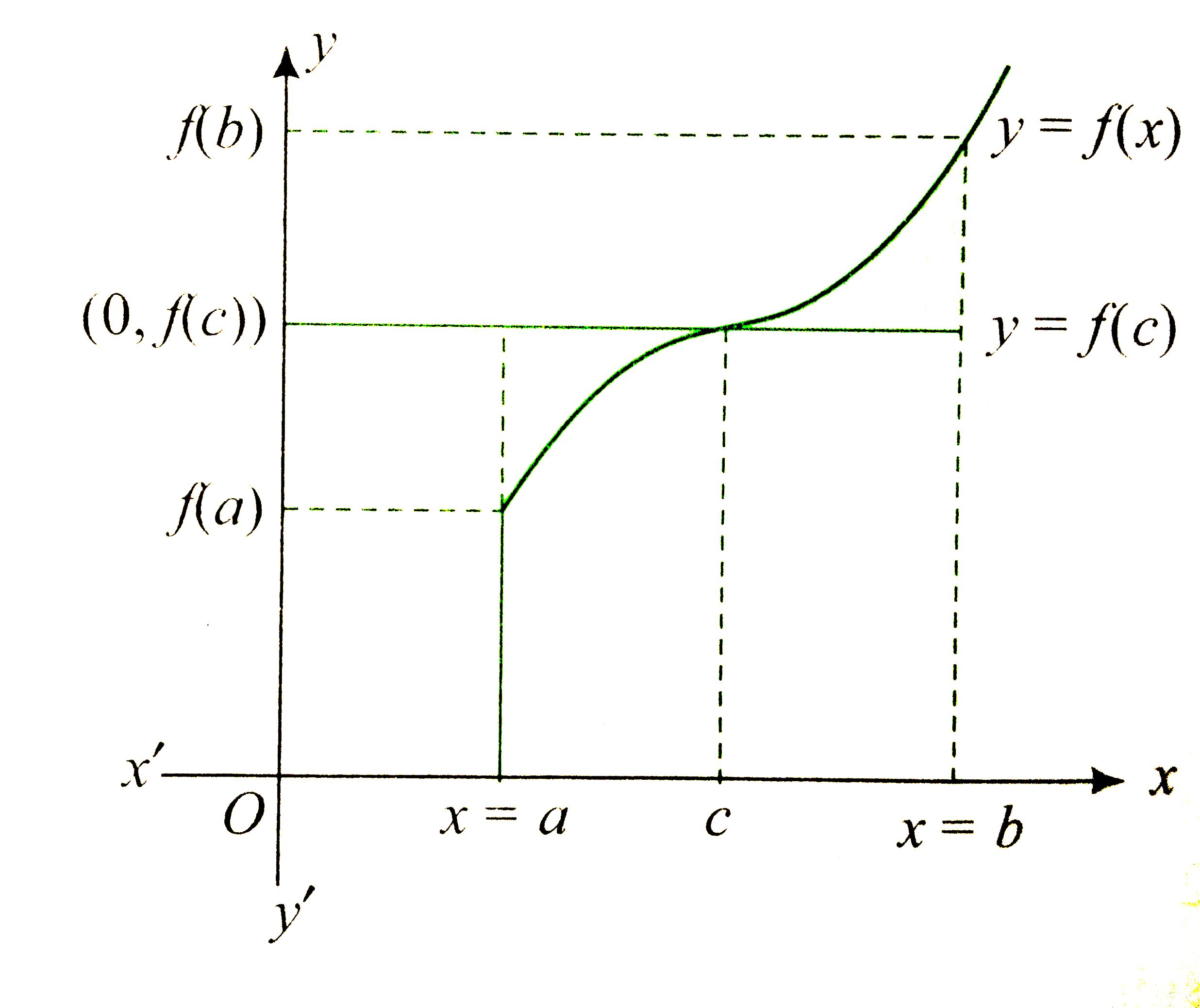
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View SolutionLet f(x)=f(a−x)andg(x)+g(a−x)=4 then ∫a0f(x)g(x)dx is equal to (A) 2∫a0f(x)dx (B) ∫a0f(x)dx (C) 4∫a0f(x)dx (D) 0
View SolutionThe value of ∫2π0√1+sin(x2)dx is a. 0 b. 4 c. 2 d. 8
View SolutionLet n∈N such that n>1.
Statement-1: ∫0∞11+xndx=∫101(1−xn)1/ndx
Statement-2: ∫baf(x)dx=∫baf(a+b−x)dx
View Solution
