If $f and g$ are the function whose graphs are as shown, let $u (x) = f (g (x)), w (x) = g (g (x))$
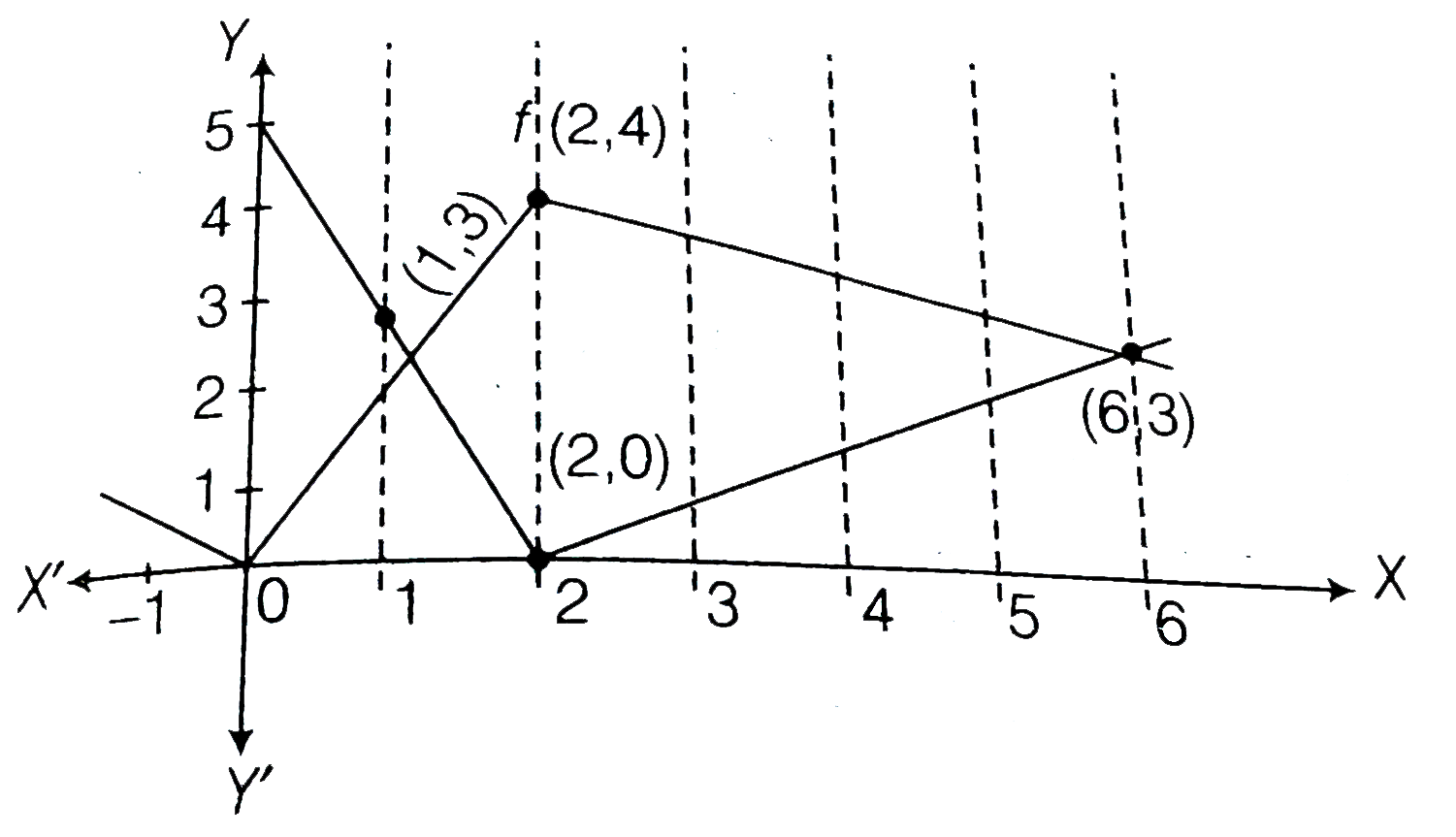Then the value of $u' (1) + w' (1)$ is

$- \frac{1}{2}$

$- \frac{3}{2}$

$- \frac{5}{4}$

does not exist

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video & image solution for If f and g are the function whose graphs are as shown, let u(x)=f(g(x)),w(x)=g(g(x)) Then the value of u'(1)+w'(1) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DIFFERENTIATION

Topper's Solved these Questions

DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise (Statement I And Ii Type Questions)
10 Videos
DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise (Passage Based Questions)
16 Videos
DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - SOLVED EXAMPLES
7 Videos
DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
26 Videos
DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos

Similar Questions

Let f be continuous and the function g is defined as $g (x) = \int_{0}^{x} (t^{2} \int_{1}^{t} f (u) d u) d t$ where $f (1) = 3$ . then the value of $g' (1) + g'' (1)$ is
View Solution
If function $f (x) = x^{2} + e^{x / 2} and g (x) = f^{- 1} (x)$ , then the value of g'(1) is
View Solution
If the function $f (x) = x^{3} + e^{\frac{x}{2}}$ and $g (x) = f^{- 1} (x)$ , then the value of $g' (1)$ is
View Solution
Suppose f and g are two functions such that f,g: R $\to$ R $f (x) = ln (1 + \sqrt{1 + x^{2}})$ and $g (x) = ln (x + \sqrt{1 + x^{2}})$ then find the value of $x e^{g (x)} f (\frac{1}{x}) + g' (x)$ at $x = 1$
View Solution
Let g be the inverse function of a differentiable function f and $G (x) = \frac{1}{g (x)} .$ If $f (4) = 2$ and $f' (4) = \frac{1}{16},$ then the value of ${(G' (2))}^{2}$ equals to:
View Solution
Let f(x) be a function satisfying $f' (x) = f (x)$ with $f (0) = 1$ and g(x) be a function that satisfies $f (x) + g (x) = x^{2}$ . Then the value of the integral $\int_{0}^{1} f (x) g (x) d x$ , is
View Solution
If f and g are continuous functions on $[0, π]$ satisfying $f (x) + f (π - x) = 1 = g (x) + g (π - x)$ then $\int_{0}^{π} [f (x) + g (x)]$ dx is equal to
View Solution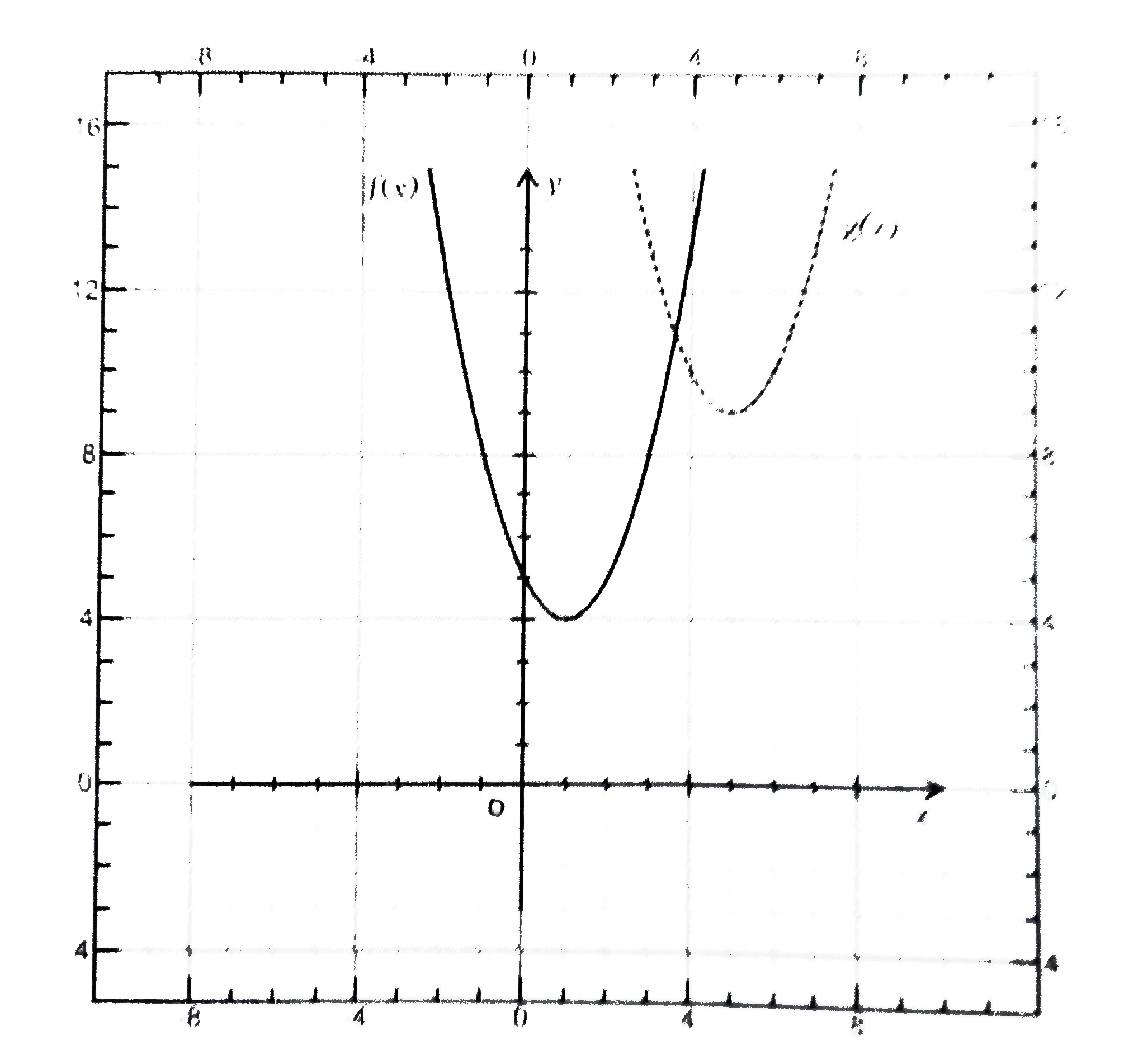
The graph of f(x) and g(x) are shown below. If g(x) = f(x + k) - m , what is the value of |k + m| ?
View Solution
Suppose f and g are differentiabel functions such that $x g (f (x)) f' (g (x)) g' (x) = f (g (x)) g' (f (x)) f' (x) \forall x \in R and f$ is positive $\forall n \in R .$ Also $\int_{0}^{x} f (g (t)) d t = \frac{1}{2} (1 - e^{- 2 x}) \forall x \in R, g (f (0)) = 1 and h (x) = \frac{g (f (x))}{f (g (x))} \forall x \in R .$
The graph of $y = h (x)$ is symmetric with respect to line:
View Solution
If the functions $f (x) = x^{3} + e^{x / 2} and g (x) = f^{- 1} (x)$ , the value of g'(1) is ………… .
View Solution

ARIHANT MATHS ENGLISH-DIFFERENTIATION -Exercise (More Than One Correct Option Type Questions)

If x=e^(y+e^(y+e^(y+...oo))),xgt0, then (dy)/(dx) is equal to
02:49
Let g be the inverse function of f and f'(x)=(x^(10))/(1+x^(2)). If g(...
02:53
If f and g are the function whose graphs are as shown, let u(x)=f(g(x)...
04:29
f'(x) = g(x) and g'(x) =-f(x) for all real x and f(5)=2=f'(5) then f^2...
03:42
If y=(f(0)f(0)f)(x)andf(0)=0,f'(0)=2 then y'(0) is equal to
02:11
If y^2=P(x) is a polynomial of degree 3, then 2(d/(dx))(y^2dot(d^2y)/(...
03:30
If y=f(x)andx=g(y) are inverse functions of each other, then
05:40
If y is a function of x then (d^2y)/(dx^2)+y \ dy/dx=0. If x is a func...
05:01
Leg g(x)=ln(f(x)), whre f(x) is a twice differentiable positive functi...
05:34
If the functions f(x)=x^(3)+e^(x//2) " and " g(x)=f^(-1)(x), the value...
01:48
Let f(theta)=sin(tan^(-1)((sintheta)/(sqrt(cos2theta)))), where -pi/4...
03:12
If y=log(sinx)(tanx), then (dy)/ (dx) at x=(1)/(4) is equal to
07:49
If y=sum(r=1)^(x) tan^(-1)((1)/(1+r+r^(2))), then (dy)/(dx) is equal t...
05:05
If y=(sin^(-1)(sinalphasinx)/(1-cosalphasinx)), then y'(0) is equal to
06:08
If f(x)=cot^(-1)((x^(x)-x^(-x))/(2)) then f'(1) equals
04:03
The function f(x)=e^x+x , being differentiable and one-to-one, has a d...
04:21
If f''(x)=-f(x) and g(x)=f^(prime)(x) and F(x)=(f(x/2))^2+(g(x/2))^2 a...
03:22
about to only mathematics
04:42
If x=f(t)cost-f^(prime)(t)sint and y=f(t)sint+f^(prime)(t)cost , then ...
07:05
If y=at^2+2bt-cand t = ax^2+2bx+c, then(d^3y)/(dx^3) equals
05:52

Home
Ask Doubt
Profile

If fandg are the function whose graphs are as shown, let u(x)=f(g(x)),w(x)=g(g(x)) Then the value of u'(1)+w'(1) is

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS ENGLISH-DIFFERENTIATION -Exercise (More Than One Correct Option Type Questions)

If $f and g$ are the function whose graphs are as shown, let $u (x) = f (g (x)), w (x) = g (g (x))$
Then the value of $u' (1) + w' (1)$ is