Let . Find the condition that is always one-one function.
The correct Answer is:
To determine the condition under which the function f(x)=ax3+bx2+cx+dsinx is always one-one, we need to analyze its derivative. A function is one-one if it is either always increasing or always decreasing. This can be established by ensuring that the derivative f′(x) is either always positive or always negative.
1. Find the derivative of the function:
f′(x)=ddx(ax3+bx2+cx+dsinx)
Using the power rule and the derivative of sine:
f′(x)=3ax2+2bx+c+dcosx
2. Set the condition for the function to be one-one:
For f(x) to be one-one, f′(x) must be either always greater than zero or always less than zero:
f′(x)>0orf′(x)<0
3. Analyze the quadratic part of the derivative:
The expression 3ax2+2bx+c is a quadratic function. The sign of this quadratic function depends on the leading coefficient 3a and the discriminant D:
D=(2b)2−4(3a)(c)=4b2−12ac
4. Condition for the quadratic to be always positive:
- If a>0, for 3ax2+2bx+c to be always positive, the discriminant must be less than zero:
D<0⇒4b2−12ac<0⇒b2<3ac
5. Consider the contribution of dcosx:
Since dcosx oscillates between −|d| and |d|, we need to ensure that even at its minimum value, f′(x) remains positive. Therefore, we must also consider:
3ax2+2bx+c+dcosx>0for all x
6. Combine conditions:
The condition for f(x) to be one-one is:
b2<3acandd must be such that 3ax2+2bx+c+dcosx>0 for all x.
Final Condition:
Thus, the condition for f(x) to be always one-one is:
b2<3acand d must be sufficiently small to ensure positivity.
f′(x)=ddx(ax3+bx2+cx+dsinx)
Using the power rule and the derivative of sine:
f′(x)=3ax2+2bx+c+dcosx
For f(x) to be one-one, f′(x) must be either always greater than zero or always less than zero:
f′(x)>0orf′(x)<0
The expression 3ax2+2bx+c is a quadratic function. The sign of this quadratic function depends on the leading coefficient 3a and the discriminant D:
D=(2b)2−4(3a)(c)=4b2−12ac
- If a>0, for 3ax2+2bx+c to be always positive, the discriminant must be less than zero:
D<0⇒4b2−12ac<0⇒b2<3ac
Since dcosx oscillates between −|d| and |d|, we need to ensure that even at its minimum value, f′(x) remains positive. Therefore, we must also consider:
3ax2+2bx+c+dcosx>0for all x
The condition for f(x) to be one-one is:
b2<3acandd must be such that 3ax2+2bx+c+dcosx>0 for all x.
Thus, the condition for f(x) to be always one-one is:
b2<3acand d must be sufficiently small to ensure positivity.
Topper's Solved these Questions
- FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:FUNCTIONSExercise:Exercise For Session 9
Explore 10 Videos
- FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:FUNCTIONSExercise:Exercise For Session 10
Explore 5 Videos
- FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:FUNCTIONSExercise:Exercise For Session 7
Explore 5 Videos
- ESSENTIAL MATHEMATICAL TOOLS Book:ARIHANT MATHS ENGLISHChapter:ESSENTIAL MATHEMATICAL TOOLS Exercise:Exercise (Single Integer Answer Type Questions)
Explore 3 Videos
- GRAPHICAL TRANSFORMATIONSBook:ARIHANT MATHS ENGLISHChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 10 Videos
Similar Questions
Let f(x) =ax3+bx2+cx+d,a≠0, where a, b, c, d∈R. If f(x) is one-one and onto, then which of the following is correct ?
View SolutionLet y=ax3+bx2+cx+d. Find the rate of change of y w.r.t x at x=0.
View SolutionLet f(X)=ax2+bx+c. Consider the following diagram
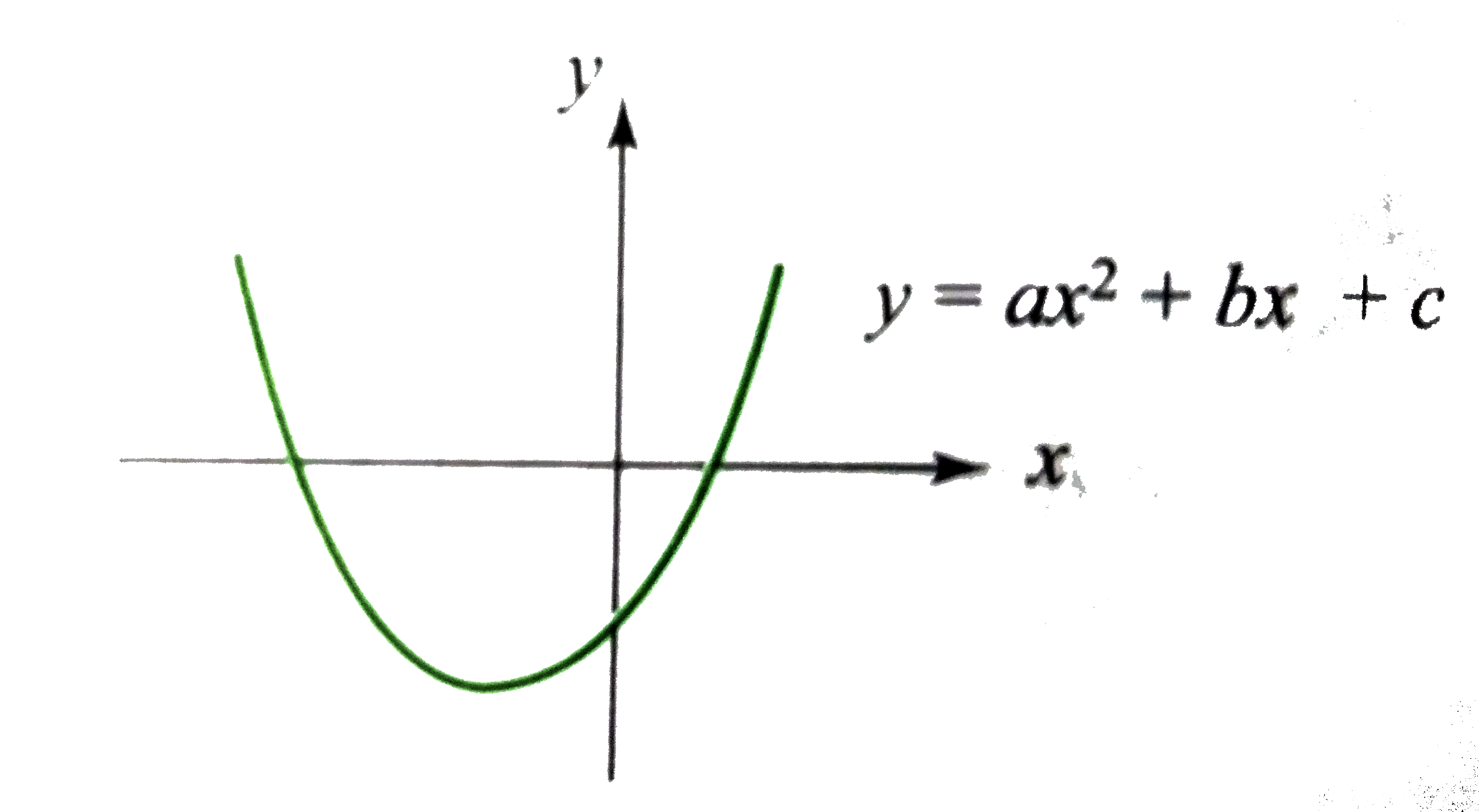 .
.
View SolutionShow that the function f(x)=3x+2 is one-one and onto
View SolutionLet f(x) =sinax+cosbx be a periodic function, then
View SolutionIf f:R→R given by f(x)=x3+px2+qx+r, is then find the condition for which f(x) is one-one.
View SolutionAssertion Letf:R→R,f(x)=x3+x2+3x+sinx f(x) is one-one. Reason f(x) is decreasing function.
View SolutionLetf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View SolutionIf f(x)=x3+3x2+12x−2sinx, where f:R→R, then (A) f(x) is many-one and onto (B) f(x) is one-one and onto(C) f(x) is one-one and into (D) f(x) is many-one and into
View SolutionIf f(x)=x3+bx2+cx+d and 0<b2<c, then
View Solution