Which of the following functions is an odd function?



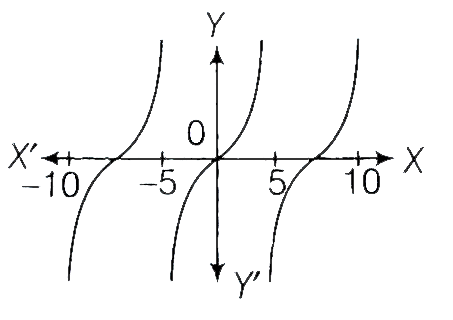
The correct Answer is:D
To determine which of the given functions is an odd function, we will follow these steps:
Step 1: Understand the Definition of an Odd Function
An odd function is defined by the property:
f(−x)=−f(x)
This means that for every point x in the domain of the function, the value of the function at −x is the negative of the value at x.
Step 2: Analyze the Graphs
We have four options (graphs) to analyze. We need to check each graph for symmetry about the origin. A graph is symmetric about the origin if, when you rotate it 180 degrees around the origin, it looks the same.
Step 3: Check Each Option
- Option 1: Check if the graph is symmetric about the origin. If it is not, it cannot be an odd function.
- Option 2: Check if the graph is symmetric about the y-axis. If it is, it is an even function, not an odd function.
- Option 3: Check for symmetry. If there is no symmetry about the origin or y-axis, it is neither odd nor even.
- Option 4: Check if the graph is symmetric about the origin. If it is, then this graph represents an odd function.
Step 4: Identify the Odd Function
After analyzing the graphs:
- Option 4 is the only graph that is symmetric about the origin, satisfying the condition for an odd function.
Conclusion
Thus, the function represented by Option 4 is an odd function.
---
An odd function is defined by the property:
f(−x)=−f(x)
This means that for every point x in the domain of the function, the value of the function at −x is the negative of the value at x.
We have four options (graphs) to analyze. We need to check each graph for symmetry about the origin. A graph is symmetric about the origin if, when you rotate it 180 degrees around the origin, it looks the same.
- Option 1: Check if the graph is symmetric about the origin. If it is not, it cannot be an odd function.
- Option 2: Check if the graph is symmetric about the y-axis. If it is, it is an even function, not an odd function.
- Option 3: Check for symmetry. If there is no symmetry about the origin or y-axis, it is neither odd nor even.
- Option 4: Check if the graph is symmetric about the origin. If it is, then this graph represents an odd function.
After analyzing the graphs:
- Option 4 is the only graph that is symmetric about the origin, satisfying the condition for an odd function.
Thus, the function represented by Option 4 is an odd function.
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)
22 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 12
4 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Knowledge Check
Which of the following functions is neither odd nor even?
A{(1,2),(4,7),(-1,2),(0,4),(-4,7)}B{(1,2),(4,7),(-1,-2),(0,0),(-4,-7)}Cy=x3−1Dy=x2−1
Which of the following functions is one-one?
View SolutionWhich of the following functions has inverse function?
View SolutionWhich of the following is a function ?
View SolutionWhich of the following function is periodic ?
View SolutionWhich of the following functions is (are) even, odd or neither:
f(x)=sinx−cosx
View SolutionWhich of the following functions is (are) even, odd or neither:
f(x)=x2sinx
View SolutionWhich of the following functions is (are) even, odd or neither:
f(x)=log(1−x1+x)
View Solution
