If r is the radius, S the surface area and V the volume of a spherical bubble, prove that
(ii)
To prove that dVdS∝r, we start by recalling the formulas for the volume V and surface area S of a sphere:
1. Volume of a sphere:
V=43πr3
2. Surface area of a sphere:
S=4πr2
Next, we need to find dVdS. We can use the chain rule for differentiation, which states that:
dVdS=dV/drdS/dr
Step 1: Differentiate V with respect to r
Using the formula for volume:
dVdr=ddr(43πr3)=4πr2
Step 2: Differentiate S with respect to r
Using the formula for surface area:
dSdr=ddr(4πr2)=8πr
Step 3: Substitute into the chain rule formula
Now we substitute the derivatives into the formula for dVdS:
dVdS=4πr28πr
Step 4: Simplify the expression
We can simplify the expression:
dVdS=4πr28πr=48⋅r2r=12r
Conclusion
Thus, we have:
dVdS=12r
This shows that dVdS is directly proportional to r, which can be expressed as:
dVdS∝r
V=43πr3
S=4πr2
dVdS=dV/drdS/dr
Using the formula for volume:
dVdr=ddr(43πr3)=4πr2
Using the formula for surface area:
dSdr=ddr(4πr2)=8πr
Now we substitute the derivatives into the formula for dVdS:
dVdS=4πr28πr
We can simplify the expression:
dVdS=4πr28πr=48⋅r2r=12r
Thus, we have:
dVdS=12r
This shows that dVdS is directly proportional to r, which can be expressed as:
dVdS∝r
Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - EXAMPLE
6 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - SINGLE OPTION CORRECT TYPE QUESTIONS
9 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
If r is the radius, S the surface area and V the volume of a spherical bubble, prove that
(i) dVdt=4πr2drdt
View SolutionA soap bubble of diameter a is produced using the soap solution of surface tension T. Find the energy required to double the radius of the bubble without change of temperature.
View Solution
Knowledge Check
If S be the surface area of V be the volume of a sphere of radius r. Then dvdt=rkdsdt. Value of k is
A12B14C2D4Which of the following is the ratio of the surface area of the sphere with radius r to its volume?
A4πB3rCr4Drπ
The weight of a body at earth's surface is W. At a depth half way to the centre of earth it will weight
View SolutionA soap bubble of radius r and surface tension 'T' is given a potential of V volt. Show that the new radius 'R' of the bubble is related to its intial radius by eqation,
p0[R3−r3]+4T[R2−r2]0−ε0V2R/2=0
where , p0 is the atmosphere pressure.
View SolutionThe work done in increasing the radius of a soap bubble from R to 3 R is
View SolutionOn heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r<<R and the surface tension of water is T, value of r just before bubbles detach is: (density of water is ρw)
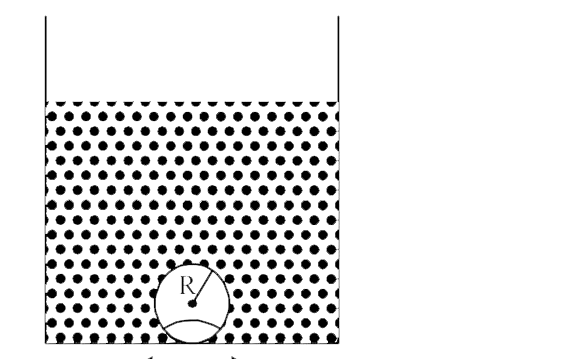
View SolutionOn heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r<<R and the surface tension of water is T, value of r just before bubbles detach is: (density of water is ρw)

View SolutionTwenty seven solid iron spheres, each of radius r and surface area S are melted toform a sphere with surface area S'.Find the(i) radius r'of the new sphere, (ii) ratio of SandS'.
View Solution
