The ends of a rod AB which is 5 m long moves along two grooves which are at right angles. If A moves 2 at a constant speed of , what is the speed of B, when it is 4 m from O?
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry
We have a rod AB of length 5 m, where point A moves along the x-axis (OX) and point B moves along the y-axis (OY). The coordinates of point A can be represented as (x, 0) and the coordinates of point B as (0, y). Since the rod is of fixed length, we can use the Pythagorean theorem to relate x and y.
Step 2: Set Up the Equation
Using the Pythagorean theorem, we have:
x2+y2=52
This simplifies to:
x2+y2=25
Step 3: Differentiate with Respect to Time
To find the relationship between the rates of change of x and y, we differentiate both sides of the equation with respect to time t:
ddt(x2)+ddt(y2)=ddt(25)
Using the chain rule, we get:
2xdxdt+2ydydt=0
Dividing through by 2 gives:
xdxdt+ydydt=0
Step 4: Substitute Known Values
We know:
- The speed of point A, dxdt=vA=12 m/s (moving away from O).
- We need to find dydt=vB when point B is 4 m from O, which means y=4.
From the Pythagorean theorem, when y=4:
x2+42=25⟹x2+16=25⟹x2=9⟹x=3 m
Step 5: Plug Values into the Differentiated Equation
Substituting x=3, y=4, and dxdt=12 into the differentiated equation:
3(12)+4dydt=0
This simplifies to:
32+4vB=0
Step 6: Solve for vB
Rearranging gives:
4vB=−32⟹vB=−38 m/s
Conclusion
The speed of point B when it is 4 m from O is:
vB=−38 m/s
The negative sign indicates that point B is moving downward along the y-axis.
We have a rod AB of length 5 m, where point A moves along the x-axis (OX) and point B moves along the y-axis (OY). The coordinates of point A can be represented as (x, 0) and the coordinates of point B as (0, y). Since the rod is of fixed length, we can use the Pythagorean theorem to relate x and y.
Using the Pythagorean theorem, we have:
x2+y2=52
This simplifies to:
x2+y2=25
To find the relationship between the rates of change of x and y, we differentiate both sides of the equation with respect to time t:
ddt(x2)+ddt(y2)=ddt(25)
Using the chain rule, we get:
2xdxdt+2ydydt=0
Dividing through by 2 gives:
xdxdt+ydydt=0
We know:
- The speed of point A, dxdt=vA=12 m/s (moving away from O).
- We need to find dydt=vB when point B is 4 m from O, which means y=4.
x2+42=25⟹x2+16=25⟹x2=9⟹x=3 m
Substituting x=3, y=4, and dxdt=12 into the differentiated equation:
3(12)+4dydt=0
This simplifies to:
32+4vB=0
Rearranging gives:
4vB=−32⟹vB=−38 m/s
The speed of point B when it is 4 m from O is:
vB=−38 m/s
The negative sign indicates that point B is moving downward along the y-axis.
Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise For Session 2
6 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise For Session 3
10 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - SINGLE OPTION CORRECT TYPE QUESTIONS
9 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
An object is moving in a circle of radius 100 m with a constant speed of 31.4m/s . What is its average speed for one complete revolution
View SolutionA 1kg stone at the end of 1m long string is whirled in a vertical circle at a constant speed of 4m/s. The tension in the string is 6N, when the stone is at (g=10m/s2)
View Solution
Knowledge Check
A 1 kg stone at the end of 1 m long string is whirled in a vertical circle at constant speed of 4 m/sec. The tension in the string is 6 N when the stone is at (g=10m/sec2)
Atop of the cirlceBbottom of the circleChalf way downDnone of the above
A car is going in south with a speed of 5m/s. To a man sitting in car a bus appears to move towards west with a speed of 2√6m/s. What is the actual speed of the bus?
View SolutionA 10cm long rod AB moves with its ends on two mutually perpendicular straight lines OX and OY . If the end A be moving at the rate of 2cm/sec, then when the distance of A from O is 8cm, the rate at which the end B is moving is
View SolutionIn the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
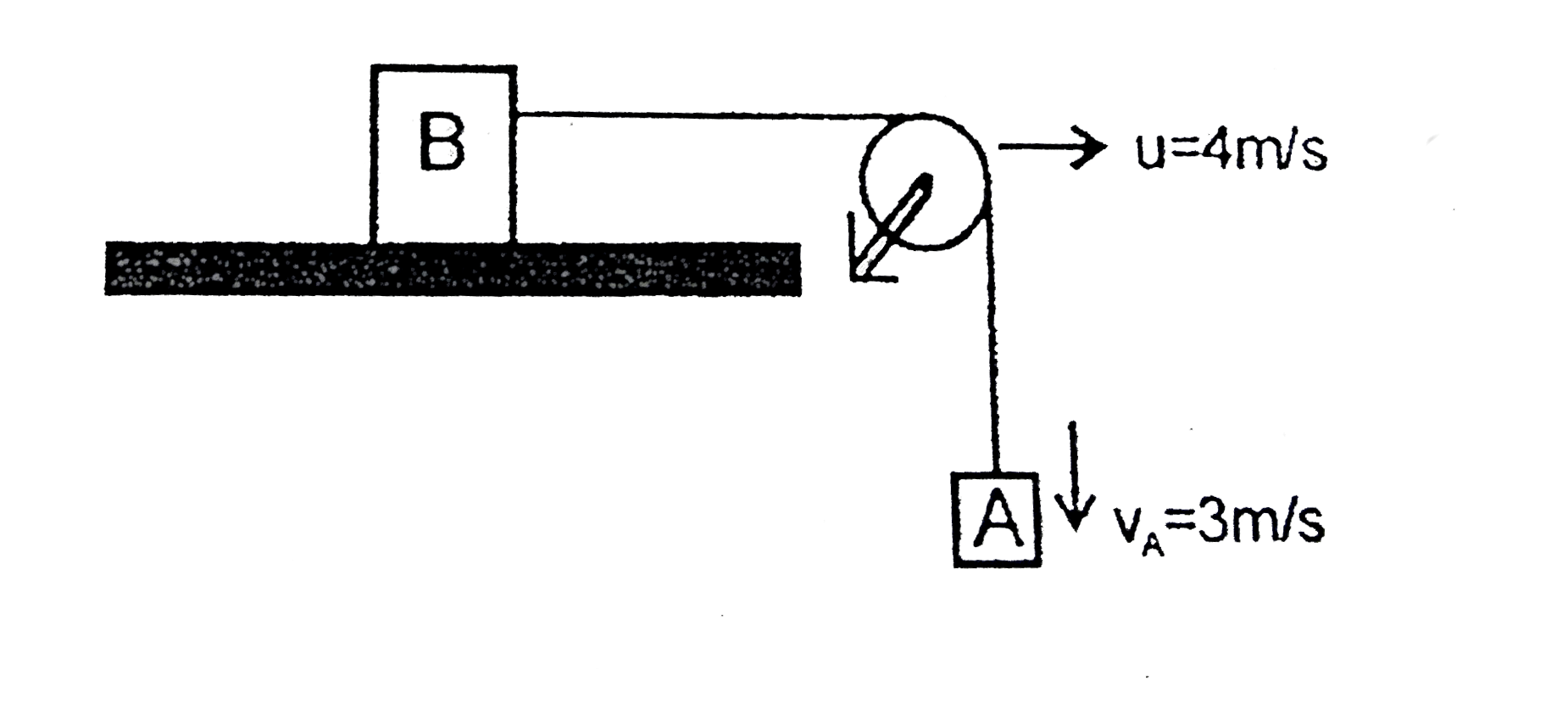
View Solution
A football is kicked with a speed of 22ms at an angle of 60∘ to the positive x direction taken along horizontal. At that instant, an observer moves past the football in a car that moves with a constant speed of 11ms is the positive x direction. Take +ve y direction vertically upwards. (g=10ms2)
View SolutionAn object moves 10 m in 4 s then turns left and moves 20 m in next 5 s. What is the average speed of the object?
View SolutionTwo particles A and B connected by a rigid rod AB. The rod slides along two perpendicular rails as shown. The velocity of A to the left is 10 m/s. What is the velocity of B, when angle θ is 37∘ ?
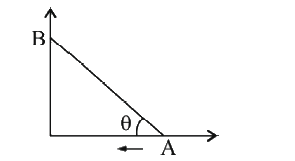
View SolutionA rod of mass 2kg and length 1m is pivoted at one end A and kept on a smooth surface. A particle of mass 500gmstrikestheotherendB of the rod and sticks to the rod. If particle was moving with the speed of 10m/s, what is the angular speed of the rod after collision ?
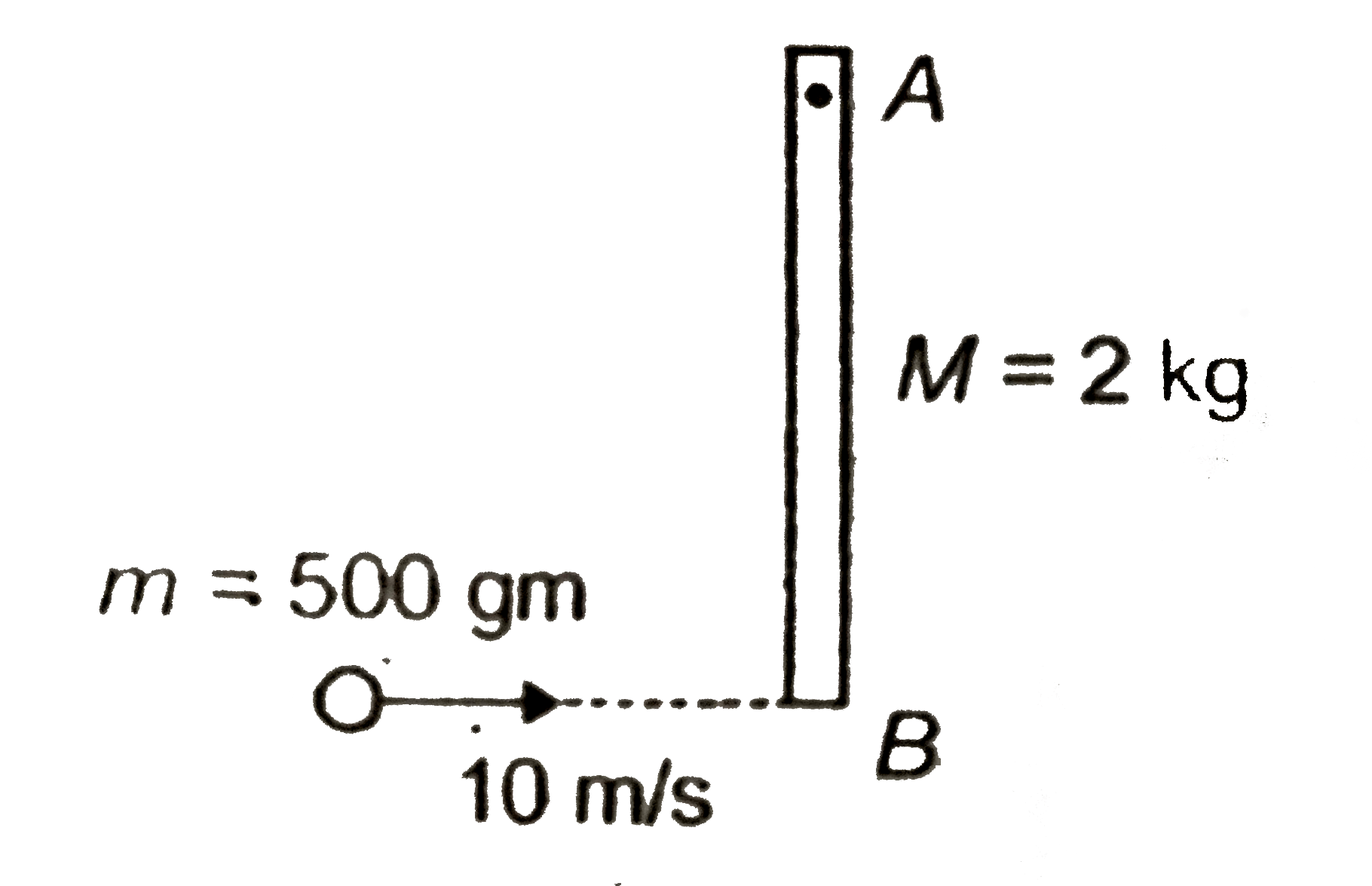
View Solution
