The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x2.
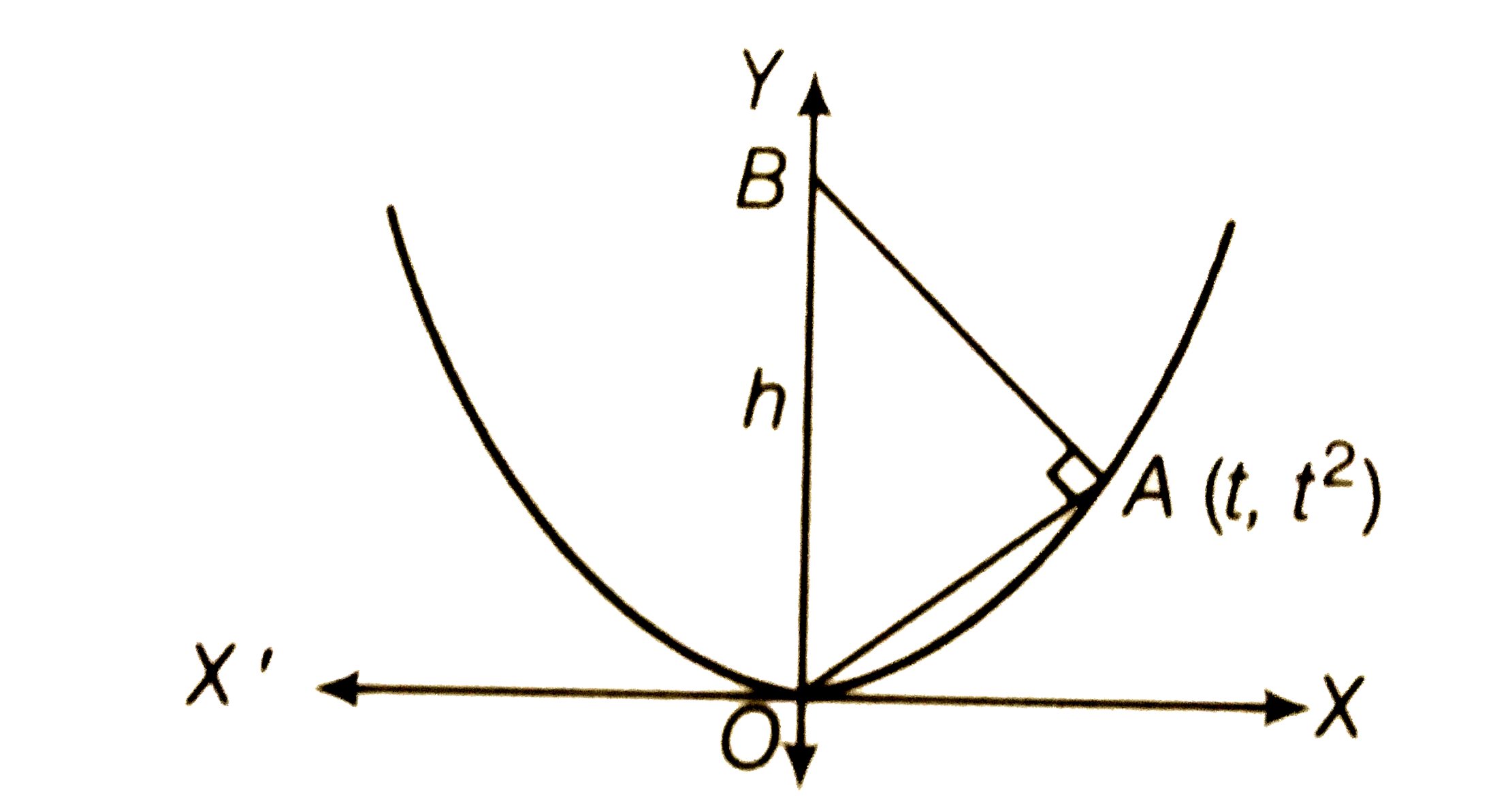
Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of limt→o(h) is equal to
0
12
1
2
The correct Answer is:C
Step by step video & image solution for The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x^(2). Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of lim_(t to o (h) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise For Session 6
4 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
Knowledge Check
The area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus rectum is
A12 sq. unitsB16 sq. unitsC18 sq.unitsD24 sq. units
If the vertex of the parabola y=x2−8x+c lies on x-axis then the value of c is
View SolutionThe parabola having its focus at (3,2) and directrix along the Y-axis has its vertex at
View SolutionIf a normal subtends a right angle at the vertex of a parabola y2=4ax then its length is
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionIf an equilateral Δ is inscribed in a parabola y2=12x with one of the vertex is at the vertex of the parabola then its height is
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose vertex is at the vertex of the parabola .Find the length of its side.
View SolutionIf the area of the triangle whose one vertex is at the vertex of the parabola, y2+4(x−a2)=0 and the other two vertices are the points of intersection of the parabola and Y-axis, is 250 sq units, then a value of 'a' is
View Solution
