Suppose that the quadratic function f(x)=ax2+bx+c is non-negative on the interval [-1,1] . Then, the area under tha graph of f over the interval [-1,1] and the X - axis is given by the formula
A=f(−1)+f(1)
A=f(−12)+f(12)
A=12[f(−1)+2f(0)+f(1)]
A=13[f(−1)+4f(0)+f(1)]
The correct Answer is:D
Step by step video & image solution for Suppose that the quadratic function f(x) = ax^(2) + bx +c is non-negative on the interval [-1,1] . Then, the area under tha graph of f over the interval [-1,1] and the X - axis is given by the formula by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Definite intefral Exercise 1 : Single Option Correct Type Questions
1 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (More Than One Correct Option Type Questions)
10 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 6
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
- DETERMINANTS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Knowledge Check
If in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
A B
B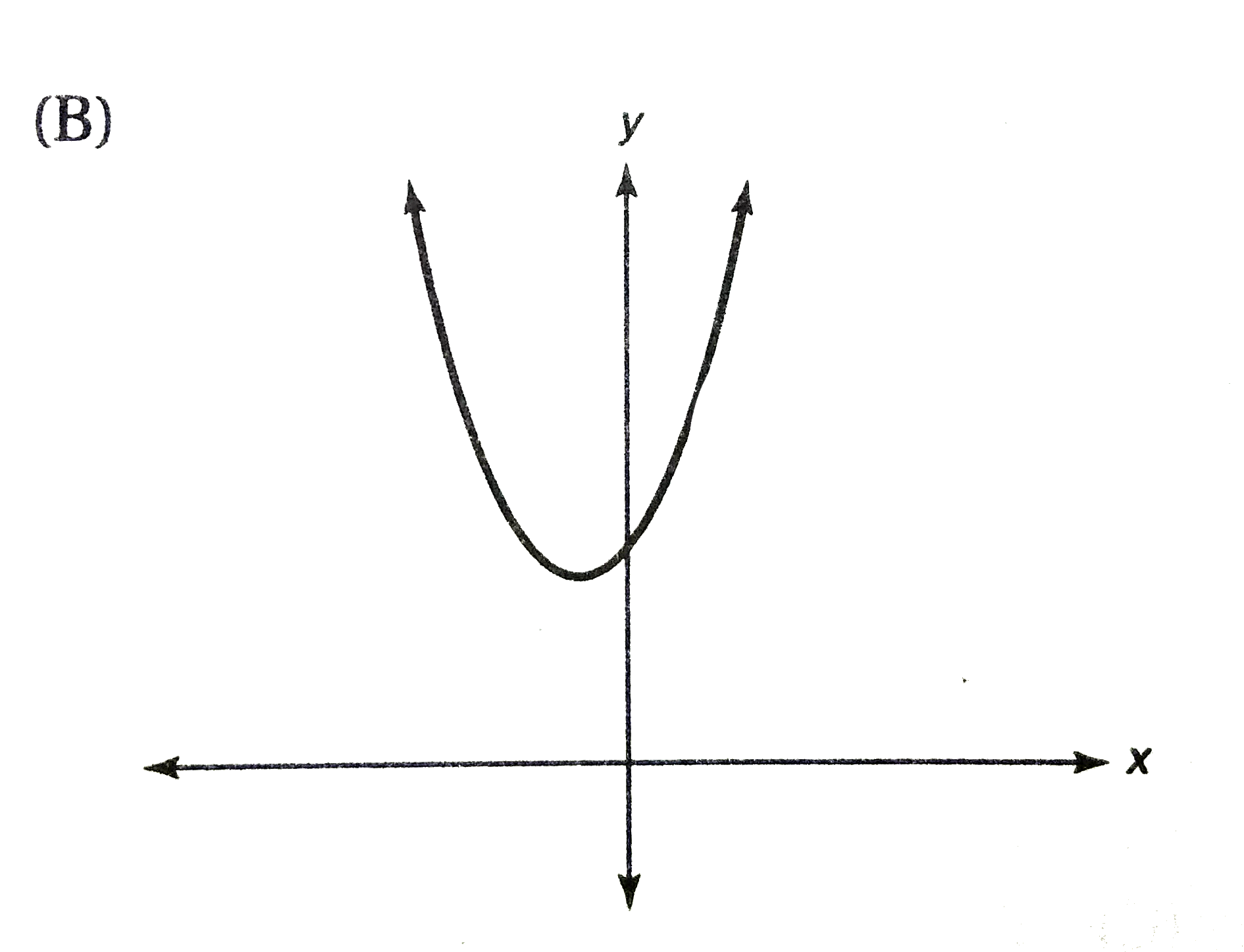 C
C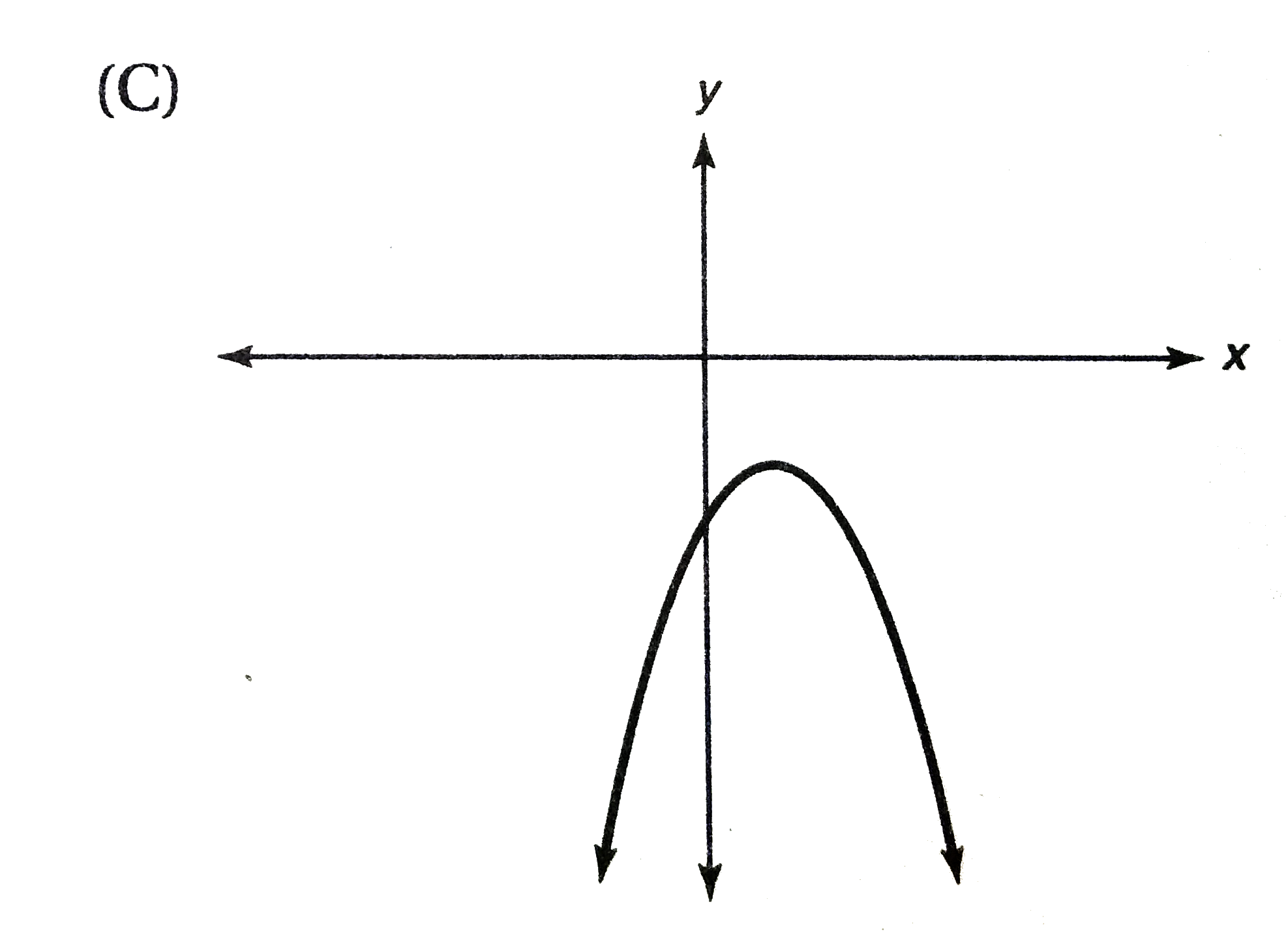 D
D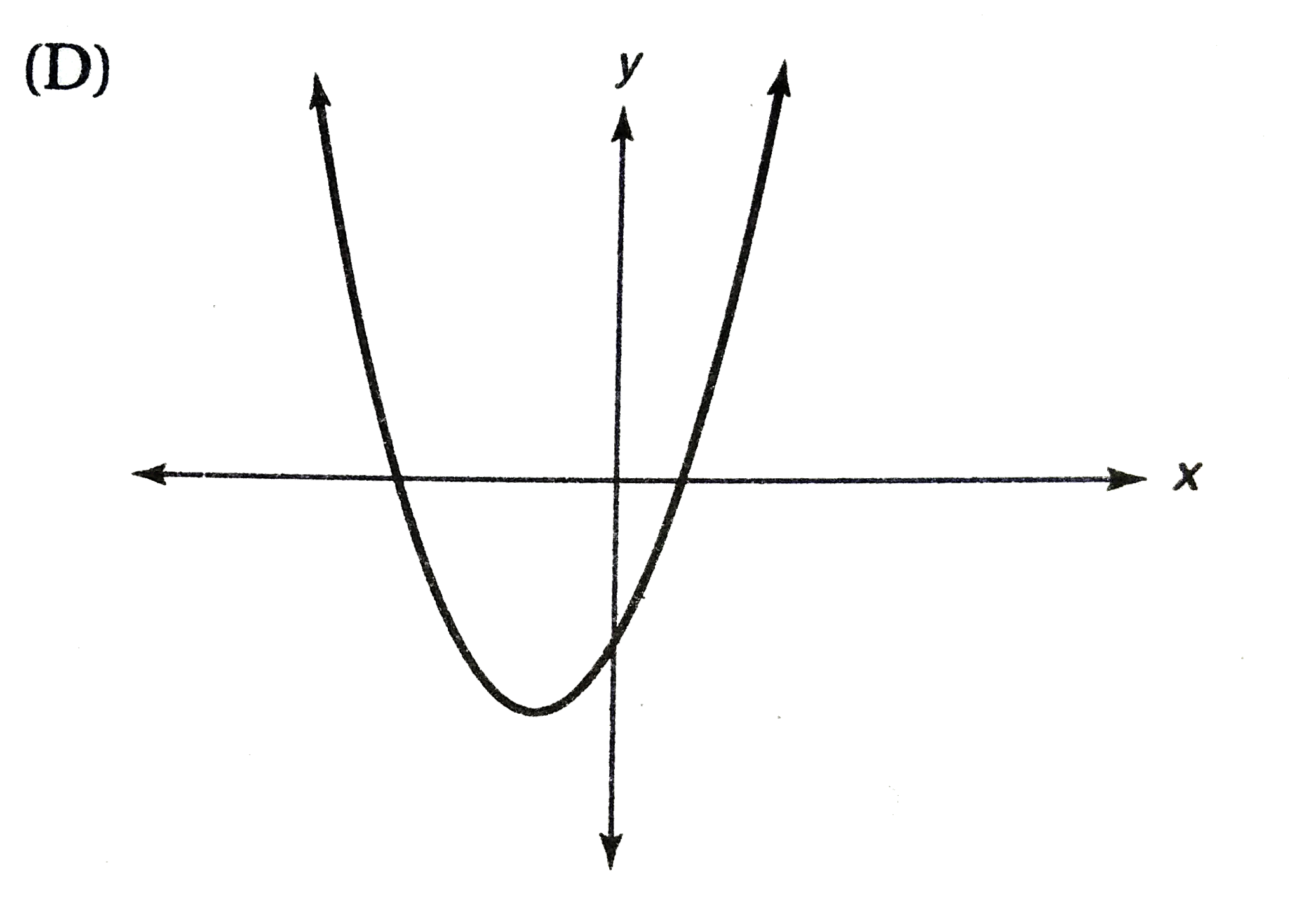
Show that the function f(x)=11+x2 is increasing function in the interval (−∞,0].
View SolutionThe function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionLet the function f(x)=x2+x+sinx−cosx+log(1+|x|) be defined on the interval [0,1]. The odd extension of f(x) to the interval [-1,1] is
View SolutionVerify Rolle's theorem for the function f(x) = x2 in the interval [−1,1].
View SolutionSuppose that f is even, periodic function with period 2, and that f(x) = x for all x in the interval [0, 1]. Then draw the graph of y = f(x).
View SolutionVerify Rolle's theorem for the function f(x) = {log (x2+2)−log3} in the interval [−1,1].
View SolutionThe greatest value of the function f(x)=2.33x−32x.4+2.3x in the interval [−1,1] is
View Solution
