Which one of the following curves represents the solution of the initial value problem dydx=100−y, where y(0)=50

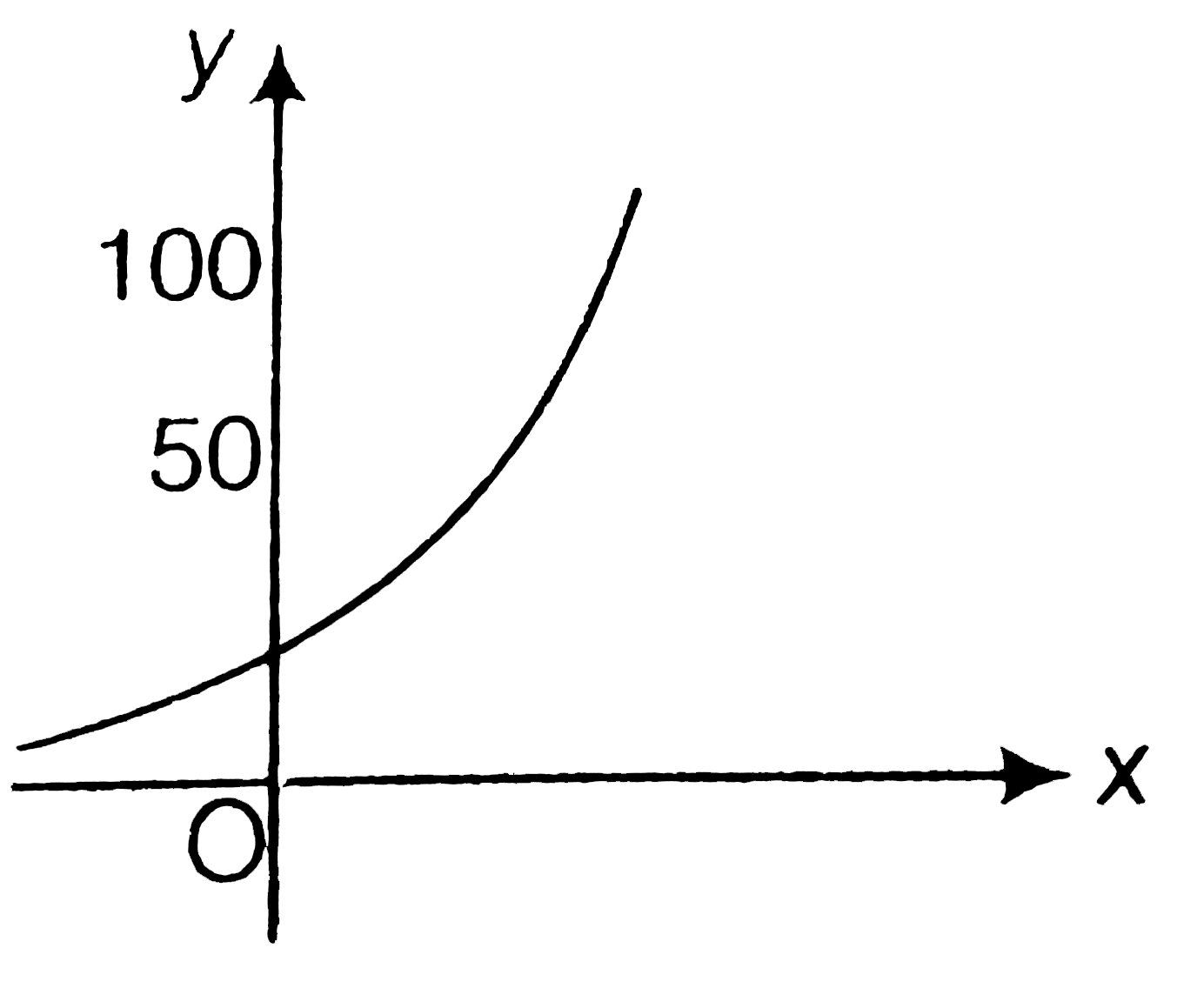
The correct Answer is:B
To solve the initial value problem given by the differential equation dydx=100−y with the initial condition y(0)=50, we can follow these steps:
Step 1: Rewrite the Differential Equation
We start with the equation:
dydx=100−y
We can rearrange this to isolate dy on one side:
dy=(100−y)dx
Step 2: Separate Variables
Next, we separate the variables by moving all terms involving y to one side and x to the other:
dy100−y=dx
Step 3: Integrate Both Sides
Now we integrate both sides. The left side requires a logarithmic integration:
∫dy100−y=∫dx
The left side integrates to:
−ln|100−y|=x+C
where C is the constant of integration.
Step 4: Solve for y
To solve for y, we first exponentiate both sides to eliminate the logarithm:
|100−y|=e−x−C
This can be rewritten as:
100−y=±e−x−C
For simplicity, we can let k=e−C (a positive constant), giving us:
100−y=ke−x
Thus, we can express y as:
y=100−ke−x
Step 5: Apply Initial Condition
Now, we apply the initial condition y(0)=50:
50=100−ke0
This simplifies to:
50=100−k⟹k=50
Step 6: Write the Final Solution
Substituting k back into the equation for y:
y=100−50e−x
Step 7: Conclusion
Thus, the solution to the initial value problem is:
y=100−50e−x
We start with the equation:
dydx=100−y
We can rearrange this to isolate dy on one side:
dy=(100−y)dx
Next, we separate the variables by moving all terms involving y to one side and x to the other:
dy100−y=dx
Now we integrate both sides. The left side requires a logarithmic integration:
∫dy100−y=∫dx
The left side integrates to:
−ln|100−y|=x+C
where C is the constant of integration.
To solve for y, we first exponentiate both sides to eliminate the logarithm:
|100−y|=e−x−C
This can be rewritten as:
100−y=±e−x−C
For simplicity, we can let k=e−C (a positive constant), giving us:
100−y=ke−x
Thus, we can express y as:
y=100−ke−x
Now, we apply the initial condition y(0)=50:
50=100−ke0
This simplifies to:
50=100−k⟹k=50
Substituting k back into the equation for y:
y=100−50e−x
Thus, the solution to the initial value problem is:
y=100−50e−x
Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (More Than One Correct Option Type Questions)
13 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Statement I And Ii Type Questions)
9 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise For Session 5
8 Videos
- DETERMINANTS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
Solve the initial value problem e(dy/dx)=x+1;y(0)=5.
View SolutionSolve the initial value problem e(dy/dx)=x+1;y(0)=5.
View SolutionSolve the initial value problem: (x+1)dydx=2e−y−1, y(0)=0
View SolutionSolve the initial value problem: cos(x+y)dy=dx,y(0)=0.
View SolutionSolve the following initial value problem: dydx=2exy3, y(0)=12
View SolutionSolve the initial value problem: dy=e2x+ydx,y(0)=0.
View SolutionSolve the initial value problem: dy=cosx (2−y cosecx)dx
View SolutionSolve the following initial value problem: xydydx=y+2, y(2)=0
View SolutionSolve the following initial value problem: dydx=ytanx, y(0)=1
View SolutionSolve the following initial value problem: dydx=1+x+y2+xy2 when y=0,x=0.
View Solution
