In a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
(a)area of the ΔXYZ is 6√6
(b)the radius of circum-circle of the ΔXYZis356√6
(c)sinX2sinY2sinZ2=435
(d)sin2(X+Y2)=35
The correct Answer is:A, C, D
To solve the problem step by step, we will follow the information provided in the question and derive the necessary values.
Step 1: Define the semi-perimeter
Given that 2s=x+y+z, we can express the semi-perimeter s as:
s=x+y+z2
Step 2: Set up the equations
From the problem statement, we have:
s−x4=s−y3=s−z2=λ
This gives us three equations:
1. s−x=4λ
2. s−y=3λ
3. s−z=2λ
Step 3: Express x,y,z in terms of λ
From the equations above, we can express x,y,z as:
- From s−x=4λ:
x=s−4λ
- From s−y=3λ:
y=s−3λ
- From s−z=2λ:
z=s−2λ
Step 4: Substitute x,y,z into the semi-perimeter equation
Substituting x,y,z into 2s=x+y+z:
2s=(s−4λ)+(s−3λ)+(s−2λ)
This simplifies to:
2s=3s−9λ
Rearranging gives:
s=9λ
Step 5: Find x,y,z in terms of λ
Now substituting s=9λ back into the equations for x,y,z:
- For x:
x=9λ−4λ=5λ
- For y:
y=9λ−3λ=6λ
- For z:
z=9λ−2λ=7λ
Step 6: Area of the triangle using the inradius
The area A of the triangle can be expressed in terms of the inradius r and the semi-perimeter s:
A=r⋅s
Given that the area of the incircle is 8π3, we can equate:
r=8π3⟹A=r⋅s=8π3⋅9λ=24πλ
Step 7: Find the circumradius R
Using the formula for the circumradius R:
R=abc4A
Substituting a=5λ,b=6λ,c=7λ and A=24πλ:
R=(5λ)(6λ)(7λ)4⋅24πλ=210λ396πλ=35λ216π
Step 8: Solve for λ
To find λ, we can use the relationship derived from the area and circumradius to check for consistency.
Final Step: Conclusion
After evaluating all equations and relationships, we can conclude with the values of x,y,z and the area of the triangle.
Given that 2s=x+y+z, we can express the semi-perimeter s as:
s=x+y+z2
From the problem statement, we have:
s−x4=s−y3=s−z2=λ
This gives us three equations:
1. s−x=4λ
2. s−y=3λ
3. s−z=2λ
From the equations above, we can express x,y,z as:
- From s−x=4λ:
x=s−4λ
- From s−y=3λ:
y=s−3λ
- From s−z=2λ:
z=s−2λ
Substituting x,y,z into 2s=x+y+z:
2s=(s−4λ)+(s−3λ)+(s−2λ)
This simplifies to:
2s=3s−9λ
Rearranging gives:
s=9λ
Now substituting s=9λ back into the equations for x,y,z:
- For x:
x=9λ−4λ=5λ
- For y:
y=9λ−3λ=6λ
- For z:
z=9λ−2λ=7λ
The area A of the triangle can be expressed in terms of the inradius r and the semi-perimeter s:
A=r⋅s
Given that the area of the incircle is 8π3, we can equate:
r=8π3⟹A=r⋅s=8π3⋅9λ=24πλ
Using the formula for the circumradius R:
R=abc4A
Substituting a=5λ,b=6λ,c=7λ and A=24πλ:
R=(5λ)(6λ)(7λ)4⋅24πλ=210λ396πλ=35λ216π
To find λ, we can use the relationship derived from the area and circumradius to check for consistency.
After evaluating all equations and relationships, we can conclude with the values of x,y,z and the area of the triangle.
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 7 : SUBJECTIVE TYPE QUESTIONS
10 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
In a triangle △XYZ, let a,b,c be the lengths o the sides opposite to the angle X,Y and Z respectively. If 1+cos2X−2cos2Y=2sinXsinY, then positive value (s) of ab is (are
View SolutionIf s−x/4= s−y/3=s-z/2 and area of incircle of the triangle XYZ is 8(pi)/3 thenThe radius of the circumcircle of △XYZ
View Solution
Knowledge Check
In triangle PQR. ∠Q is a right angle, QR=24, and PR=26. Triangle YXZ is similar to triangle PQR, where vertices X, Y, and Z correspond to vertices P, Q, and R, respectively, and each side of triangle XYZ is 12 the length of the corresponding side of triangle PQR. What is the value of sin Z?
A513B512C1213D125
In a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
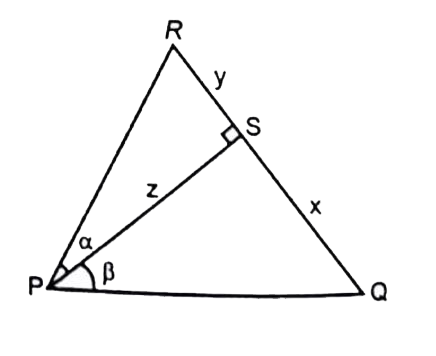
View SolutionIf in ΔABC, the distance of the vertices from the orthocenter are x,y, and z then prove that ax+by+cz=abcxyz
View SolutionIn a ΔPQR as show in figure given that x:y:z::2:3:6, then find value of ∠QPR.
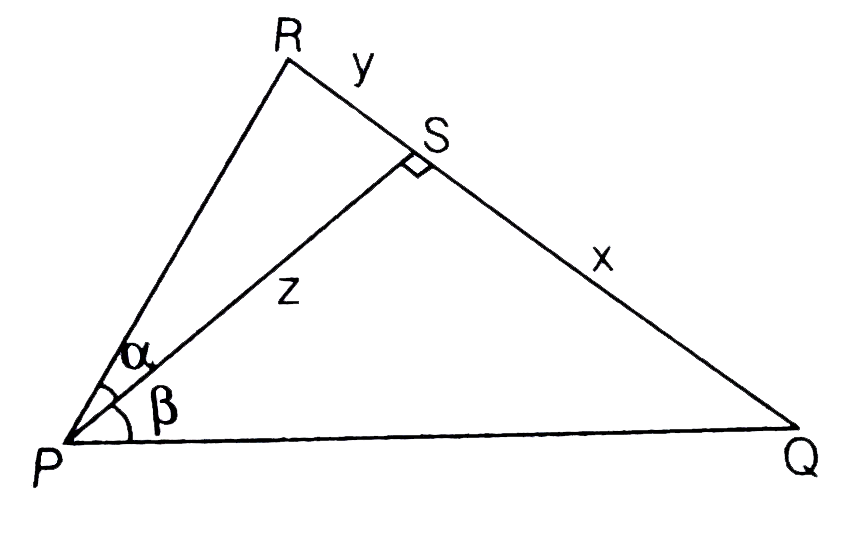
View SolutionFind the perimeter of a triangle whose sides are 2y+3z,z−y,4y−2z.
View SolutionLet x,y,z are positive reals and x+y+z=60andx>3.
Maximum value of xyz is :
View SolutionFind the coordinates of the centroid of the triangle whose vertices are (x1,y1,z1), (x2,y2,z2)and (x3,y3,z3).
View SolutionIf xyz=1 and x,y,z>0 then the minimum value of the expression (x+2y)(y+2z)(z+2x) is
View Solution
