The correct Answer is:(A)→(r,s);(B)→(t);(C)→(p,q)
(A) ∵(√2+31/5)10=(21/2+31/5)10
∴Tr+1=10Cr⋅210−r2⋅3r5
For rational terms, r = 0, 10 [∵0≤r≤10]
∴ Number of rational terms = 2
i.e., m = 2 and (√3+51/8)256=(31/2+51/8)256
∴TR+10=256CR⋅3256−R2⋅5R/8
For rational terms, r = 0, 8, 16, 24, 32, ..., [∵0≤r≤256]
∴ Number of rational terms = 1 + 32 = 33
i.e., n=33⇒m+n=35(s)andn−m=31
(B) Tr+1in(21/3+31/5)40=40Cr⋅240−r3⋅3r/5
For rational terms, r = 10, 25, 40 [∵0≤r≤40]
∵ Number of rational terms = 3
∴ Number of irrational terms
= Total terms - Number of rational terms
= 41 - 3 = 38 i.e. m = 38
and TR−1in(51/10+21/6)100=100CR⋅5100−R10⋅2R/6
rational terms, R =0, 30 , 60, 90 [∵0≤R≤100]
∵ Number of rational terms = 4
∴ Number of irrational terms = 101 - 4 = 97
i.e n=97⇒m+n=100,n−m=97−38=39
(C) ∵(1+√2+31/3)6=(1+21/2+31/3)6
=∑α+β+γ=66!α!β!γ!(1)α(21/2)β(31/3)γ
=∑α+β+γ=66!α!β!γ!2β/2⋅3γ/3
Values of (α,β,γ) for rational terms are (0, 0, 6)
(1, 2, 3), (3, 0, 3), (0, 6, 0), (2, 4, 0), (4, 2, 0), (6, 0, 0).
∴ Number of rational terms = 7 i.e., m = 7
and (1+3√2+5√3)15=(1+21/3+31/5)15
=∑α+β+γ=1515!α!β!γ!(1)α(21/3)β(31/5)γ
=∑α+β+γ=1515!α!β!γ!2β/3⋅3γ/5
of (α,β,γ) for rational terms are
95, 0, 10), (2, 3, 10), (10, 0, 5), (7, 3, 5), (4, 6, 5), (1, 9, 5),
(15, 0, 0), (12, 3, 0), (9, 6, 0), (6, 9, 0), (3, 12, 0), (15, 0, 0).
∴ Number of rational termas = 13 i.e. n = 13
Hence, m+n=20andn−m=6
Topper's Solved these Questions
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 1
7 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 2
7 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- AREA OF BOUNDED REGIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
23 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
Similar Questions
The value of 10∑r=0r10Cr3r(−2)10−r is 20 b. 10 c. 300 d. 30
View Solutionabout to only mathematics
View SolutionThe value of (300)(3010)−(301)(3011)+(302)(3012)++(3020)(3030)= a. ^60C20 b. ^30C10 c. ^60C30 d. ^40C30
View SolutionArea of the region
{(x,y)∈R2:y≥√|x+3|,5y≤x+9≤15} is equal to
View Solutionabout to only mathematics
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
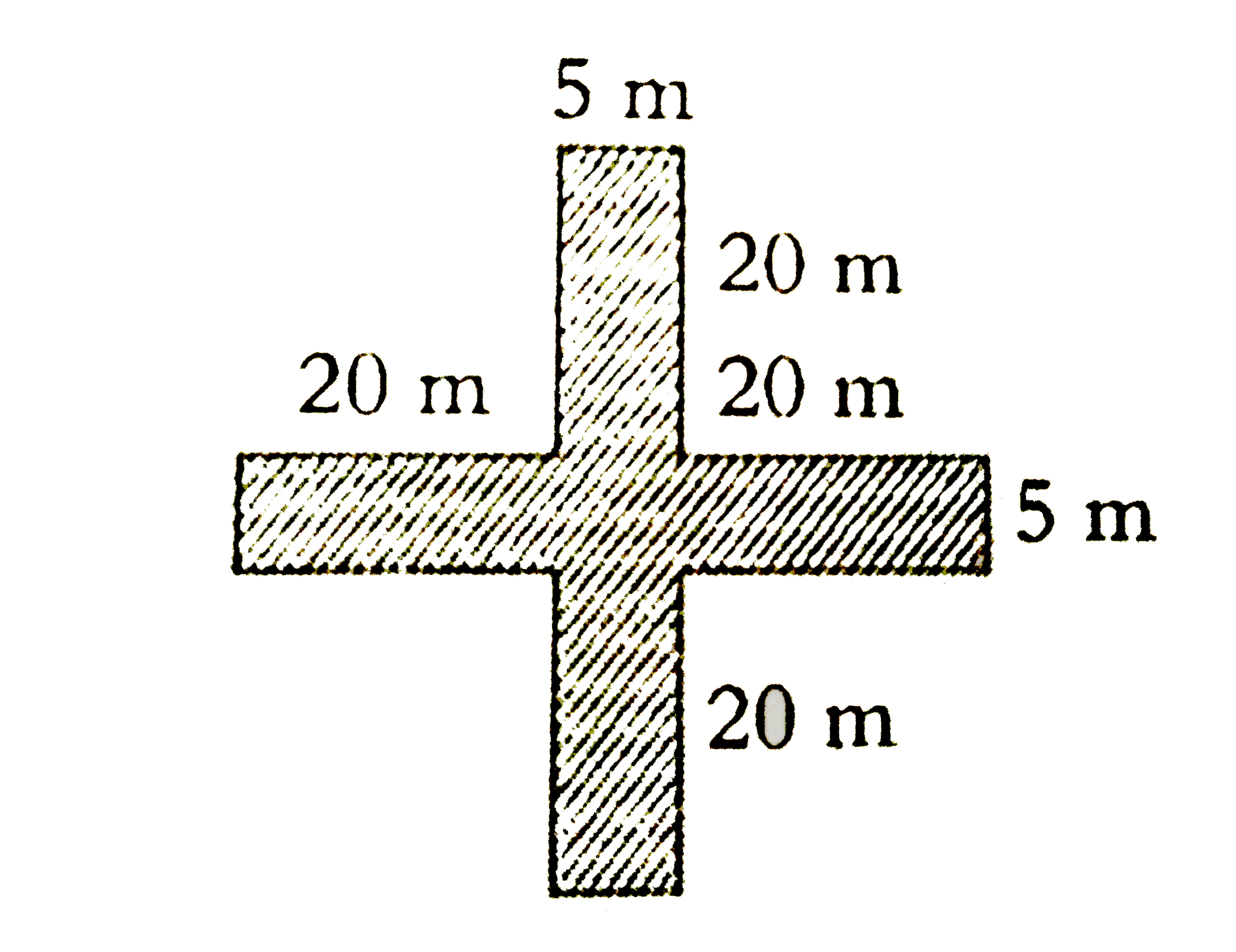
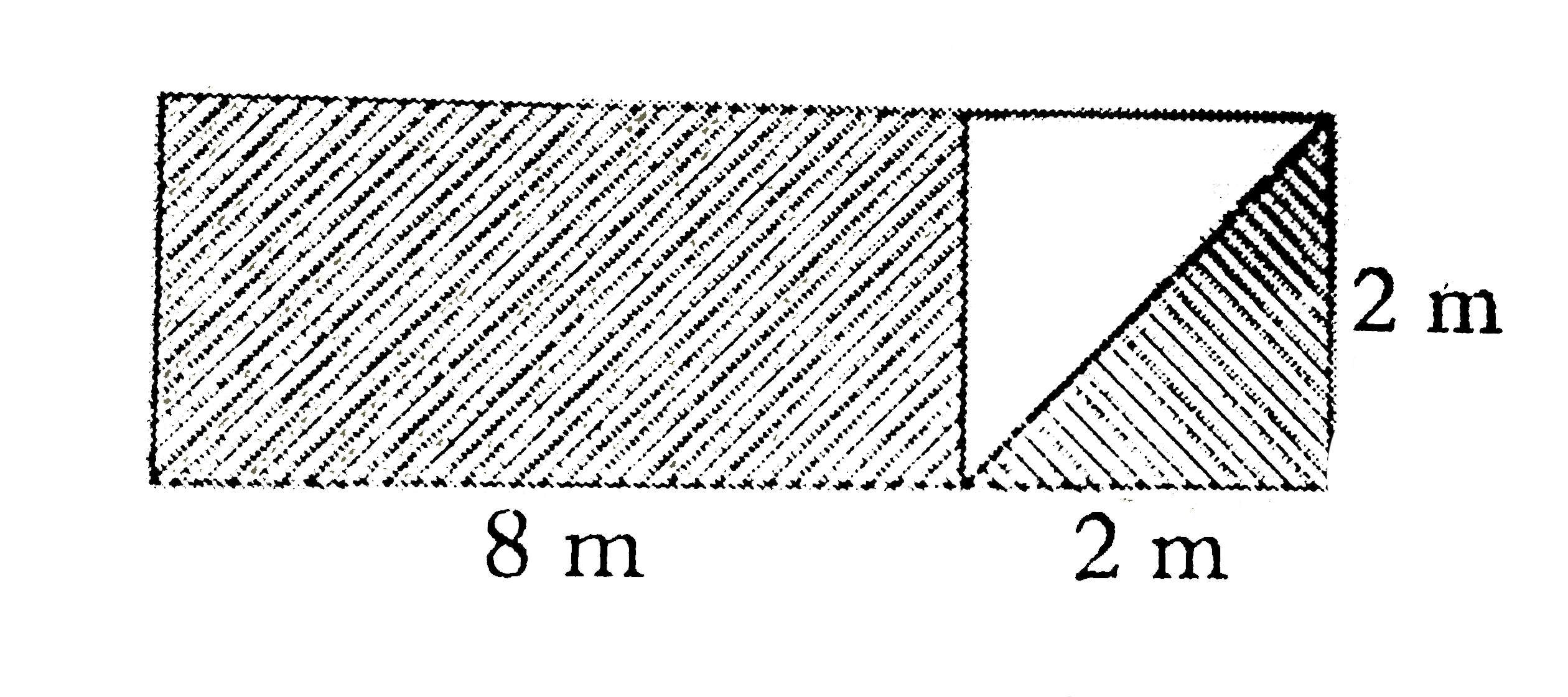
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

