If A, B, C, be the centres of three co-axial circles and $t_{1}, t_{2}, t_{3}$ be the lengths of the tangents of them any piont, prove that
$¯ ¯¯¯¯ ¯ B C . t_{1}^{2} + ¯ ¯¯¯¯ ¯ C A . t_{2}^{2} + ¯ ¯¯¯¯ ¯ A B . t_{3}^{2} = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:which proves the result.

Updated on:21/07/2023

Answer

Step by step video & image solution for If A, B, C, be the centres of three co-axial circles and t_(1),t_(2),t_(3) be the lengths of the tangents of them any piont, prove that bar(BC).t_(1)^(2)+bar(CA).t_(2)^(2)+bar(AB).t_(3)^(2)=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise For Session 1
18 Videos
CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise For Session 2
17 Videos
BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos

Similar Questions

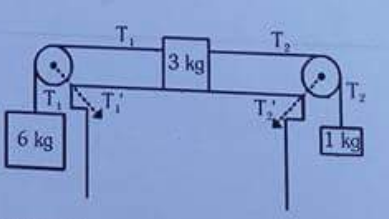
Calculate a, $T_{1}, T_{2}, T_{1}' & T_{2}'$ .
View Solution
The base of a triangle is divided into three equal parts. If $t_{1}, t_{2}, t_{3}$ are the tangents of the angles subtended by these parts at the opposite vertex, prove that $(\frac{1}{t_{1}} + \frac{1}{t_{2}}) (\frac{1}{t_{2}} + \frac{1}{t_{3}}) = 4 (1 + \frac{1}{t 22}) .$
View Solution
If $A$ is the centre of the circle, $x^{2} + y^{2} + 2 g_{i} x + 5 = 0$ and $t_{i}$ is the length of the tangent from any point to this circle, $i = 1, 2, 3,$ then show that $(g_{2} - g_{3}) t_{1}^{2} + (g_{3} - g_{1}) t_{2}^{2} + (g_{1} - g_{2}) t_{3}^{2} = 0$
View Solution
The length of the transversal common tangent to the circle $x^{2} + y^{2} = 1$ and ${(x - t)}^{2} + y^{2} = 1$ is $\sqrt{21}$ , then t=
View Solution
If $t_{1}, t_{2} and t_{3}$ are distinct, the points $(t_{1} 2 a t_{1} + a t_{1}^{3}), (t_{2}, 2 {at}_{2} + a t_{2}^{3}) and (t_{3}, 2 a t_{3} + a t_{3}^{3})$
View Solution
A tank full of water has a small hole at its bottom. Let $t_{1}$ be the time taken to empty first one third of the tank and $t_{2}$ be the time taken to empty second one third of the tank and $t_{3}$ be the time taken to empty rest of the tank then
(a). $t_{1} = t_{2} = t_{3}$
(b). $t_{1} > t_{2} > t_{3}$
(c). $t_{1} < t_{2} < t_{3}$
(d). $t_{1} > t_{2} < t_{3}$
View Solution
Find the slope of the tangent to the curve $x = t^{2} + 3 t - 8$ , $y = 2 t^{2} - 2 t - 5$ at $t = 2$ .
View Solution
Let C be incircle of $Δ A B C$ . If the tangents of lengths $t_{1}, t_{2} and t_{3}$ are drawn inside the given triangle parallel to side a,b, and c, respectively, then $\frac{t_{1}}{a} + \frac{t_{2}}{b} + \frac{t_{3}}{c}$ is equal to
View Solution
If $t_{1}, t_{2}, t_{3}$ are the feet of normals drawn from $(x_{1}, y_{1})$ to the parabola $y^{2} = 4 a x$ then the value of $t_{1} t_{2} t_{3}$ =
View Solution
I , II , III are three isotherms respectively at $T_{1}, T_{2}, T_{3}$ . Temperature will be in order

View Solution

ARIHANT MATHS ENGLISH-CIRCLE -Exercise (Questions Asked In Previous 13 Years Exam)

If A, B, C, be the centres of three co-axial circles and t(1),t(2),t(3...
05:08
about to only mathematics
04:09
If the circles x^2+y^2+2a x+c y+a=0 and points Pa n dQ , then find the...
04:56
A circle touches the x-axis and also touches the circle with center (0...
05:08
about to only mathematics
04:28
Let ABCD be a square of side length 2 units. C2 is the circle through ...
06:10
ABCD is a square of side length 2 units. C(1) is the circle touching ...
03:13
ABCD is a square of side length 2 units. C(1) is the circle touching ...
02:29
about to only mathematics
03:58
Let C be the circle with centre (0, 0) and radius 3 units. The equatio...
03:00
Tangents are drawn from the point (17, 7) to the circle x^2+y^2=169, ...
03:45
Consider a family of circles which are passing through the point (-1,1...
04:50
A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
12:56
A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
12:56
A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
12:56
Consider: L1:2x+3y+p-3=0 L2:2x+3y+p+3=0 where p is a real number and...
08:37
The point diametrically opposite to the point P(1, 0) on the circle x^...
05:31

Home
Ask Doubt
Profile

If A, B, C, be the centres of three co-axial circles and t1,t2,t3 be the lengths of the tangents of them any piont, prove that ¯¯¯¯¯¯BC.t21+¯¯¯¯¯¯CA.t22+¯¯¯¯¯¯AB.t23=0

The correct Answer is:which proves the result.

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS ENGLISH-CIRCLE -Exercise (Questions Asked In Previous 13 Years Exam)

If A, B, C, be the centres of three co-axial circles and $t_{1}, t_{2}, t_{3}$ be the lengths of the tangents of them any piont, prove that
$¯ ¯¯¯¯ ¯ B C . t_{1}^{2} + ¯ ¯¯¯¯ ¯ C A . t_{2}^{2} + ¯ ¯¯¯¯ ¯ A B . t_{3}^{2} = 0$