The sides of a rectangle are given by the equations x=-2, x = 4, y=-2 andy=5. Find the equation of the circle drawn on the diagonal of this rectangle as its diameter.
The correct Answer is:A, B, C
To find the equation of the circle drawn on the diagonal of the rectangle as its diameter, we can follow these steps:
Step 1: Identify the vertices of the rectangle
The sides of the rectangle are given by the equations:
- x=−2
- x=4
- y=−2
- y=5
The vertices of the rectangle can be determined by the intersection of these lines:
- Bottom-left vertex: (−2,−2)
- Bottom-right vertex: (4,−2)
- Top-left vertex: (−2,5)
- Top-right vertex: (4,5)
Step 2: Identify the endpoints of the diagonal
The diagonal of the rectangle can be taken as the line segment connecting the bottom-left vertex A(−2,−2) and the top-right vertex B(4,5).
Step 3: Find the midpoint of the diagonal
The midpoint M of the diagonal AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(−2+42,−2+52)=(22,32)=(1,1.5)
Step 4: Calculate the radius of the circle
The radius r of the circle is half the length of the diagonal AB. The length of the diagonal can be calculated using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of points A and B:
AB=√(4−(−2))2+(5−(−2))2=√(4+2)2+(5+2)2=√62+72=√36+49=√85
Thus, the radius r is:
r=AB2=√852
Step 5: Write the equation of the circle
The standard equation of a circle with center (h,k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting h=1, k=1.5, and r=√852:
(x−1)2+(y−32)2=(√852)2
Calculating r2:
r2=(√852)2=854
Thus, the equation of the circle is:
(x−1)2+(y−32)2=854
Final Answer
The equation of the circle drawn on the diagonal of the rectangle as its diameter is:
(x−1)2+(y−32)2=854
The sides of the rectangle are given by the equations:
- x=−2
- x=4
- y=−2
- y=5
- Bottom-left vertex: (−2,−2)
- Bottom-right vertex: (4,−2)
- Top-left vertex: (−2,5)
- Top-right vertex: (4,5)
The diagonal of the rectangle can be taken as the line segment connecting the bottom-left vertex A(−2,−2) and the top-right vertex B(4,5).
The midpoint M of the diagonal AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(−2+42,−2+52)=(22,32)=(1,1.5)
The radius r of the circle is half the length of the diagonal AB. The length of the diagonal can be calculated using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of points A and B:
AB=√(4−(−2))2+(5−(−2))2=√(4+2)2+(5+2)2=√62+72=√36+49=√85
Thus, the radius r is:
r=AB2=√852
The standard equation of a circle with center (h,k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting h=1, k=1.5, and r=√852:
(x−1)2+(y−32)2=(√852)2
Calculating r2:
r2=(√852)2=854
Thus, the equation of the circle is:
(x−1)2+(y−32)2=854
The equation of the circle drawn on the diagonal of the rectangle as its diameter is:
(x−1)2+(y−32)2=854
Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise For Session 3
16 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise For Session 4
16 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise For Session 1
18 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos
Similar Questions
The sides of a square are x=2,x=3,y=1andy=2. Find the equation of the circle drawn on the diagonals of the square as its diameter.
View SolutionThe sides of a square are x=1,x=3,y=2andy=4.Find the equation of the circle drawn on the diagonal of the square as its diameter.
View SolutionFind the equaiton of the circle drawn on a diagonal of the rectangle as its diameter whose sides are : x=5,x=8,y=4,y=7
View SolutionThe sides of a square are x=6, x=9, y=3 and y=6. Find the equation of a circle drawn on the diagonal of the square as its diameter.
View SolutionFind the equations of the circles drawn on the diagonals of the rectangle as its diameter whose sides are x=5, x=−2, y=3 and y=−1.
View SolutionFind the length of the diagonal of a rectangle whose sides are 12cm and 5cm.
View SolutionFind the equation of the circle drawn on the intercept made by the line 2x+3y=6 between the coordinate axes as diameter.
View SolutionThe sides of a rectangle are x and y, respectively. Find the rule for finding the perimeter of the rectangle.
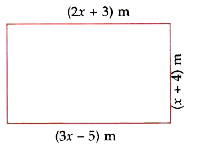
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
View SolutionThe adjacent sides of a rectangle are 3x2−2xy+5y2 and 2x2+5xy−3y2. Find the area of the rectangle.
View Solution