Which of the following equations in parametric form can represent a hyperbola, where t is a parameter?
A:x=a2(t+1t)andy=b2(t−1t)
B:txa−yb+t=0andxa+tyb−1=0
C:x=et+e−tandy=et−e−t
D:x2−6=2costandy2+2=4cos2(t2)
The correct Answer is:A, C, D
To determine which of the given parametric equations represents a hyperbola, we will analyze each option step by step.
Step 1: Analyze Option A
The equations are:
- x=a2T+1T
- y=b2T−1T
1.1 Rewrite x and y in terms of T:
- xa2=T+2aT
- yb2=T−2bT
1.2 Square both equations:
- (xa2)2=(T+2aT)2
- ⎛⎝yb2⎞⎠2=(T−2bT)2
1.3 Expand and simplify:
- x2a24=T2+2+4a2T2
- y2b24=T2−2+4b2T2
1.4 Combine the equations:
- x2a24−y2b24=1
Conclusion for A: This represents a hyperbola.
Step 2: Analyze Option B
The equations are:
- Txa−yb+T=0
- xa+Tyb−1=0
2.1 Rearranging gives:
- Tx=yb−T
- x=a(1−Tyb)
2.2 Substitute x into the first equation and simplify:
- This leads to a quadratic form that does not yield the hyperbola form.
Conclusion for B: This does not represent a hyperbola.
Step 3: Analyze Option C
The equations are:
- x=eT+e−T
- y=eT−e−T
3.1 Square both equations:
- x2=(eT+e−T)2=e2T+2+e−2T
- y2=(eT−e−T)2=e2T−2+e−2T
3.2 Combine:
- x2−y2=4
3.3 Rewrite:
- x24−y24=1
Conclusion for C: This represents a hyperbola.
Step 4: Analyze Option D
The equations are:
- x2−6=2cosT
- y2+2=4cos2T2
4.1 Rearranging gives:
- x2=2cosT+6
- y2=4cos2T2−2
4.2 Use trigonometric identities to combine:
- This leads to the form x2−y2=6.
4.3 Rewrite:
- x26−y26=1
Conclusion for D: This represents a hyperbola.
Final Conclusion
The equations that represent a hyperbola are:
- Option A
- Option C
- Option D
The equations are:
- x=a2T+1T
- y=b2T−1T
- xa2=T+2aT
- yb2=T−2bT
- (xa2)2=(T+2aT)2
- ⎛⎝yb2⎞⎠2=(T−2bT)2
- x2a24=T2+2+4a2T2
- y2b24=T2−2+4b2T2
- x2a24−y2b24=1
The equations are:
- Txa−yb+T=0
- xa+Tyb−1=0
- Tx=yb−T
- x=a(1−Tyb)
- This leads to a quadratic form that does not yield the hyperbola form.
The equations are:
- x=eT+e−T
- y=eT−e−T
- x2=(eT+e−T)2=e2T+2+e−2T
- y2=(eT−e−T)2=e2T−2+e−2T
- x2−y2=4
- x24−y24=1
The equations are:
- x2−6=2cosT
- y2+2=4cos2T2
- x2=2cosT+6
- y2=4cos2T2−2
- This leads to the form x2−y2=6.
- x26−y26=1
The equations that represent a hyperbola are:
- Option A
- Option C
- Option D
Topper's Solved these Questions
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise (Passage Based Questions)
14 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise (Single Option Correct Type Questions)
30 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Knowledge Check
Which of the following is (are) a pair of parametric equation that represent a circle?
{x=sinθy=cosθ
{x=ty=√1−t2
{x=√sy=√1−sAonly IBonly IIConly IIIDonly II and IIIIf 0≤t≤1, which of the following graphs is the graph of y versus x where x and y are related by the parametric equations y=t2 and x=√t ?
A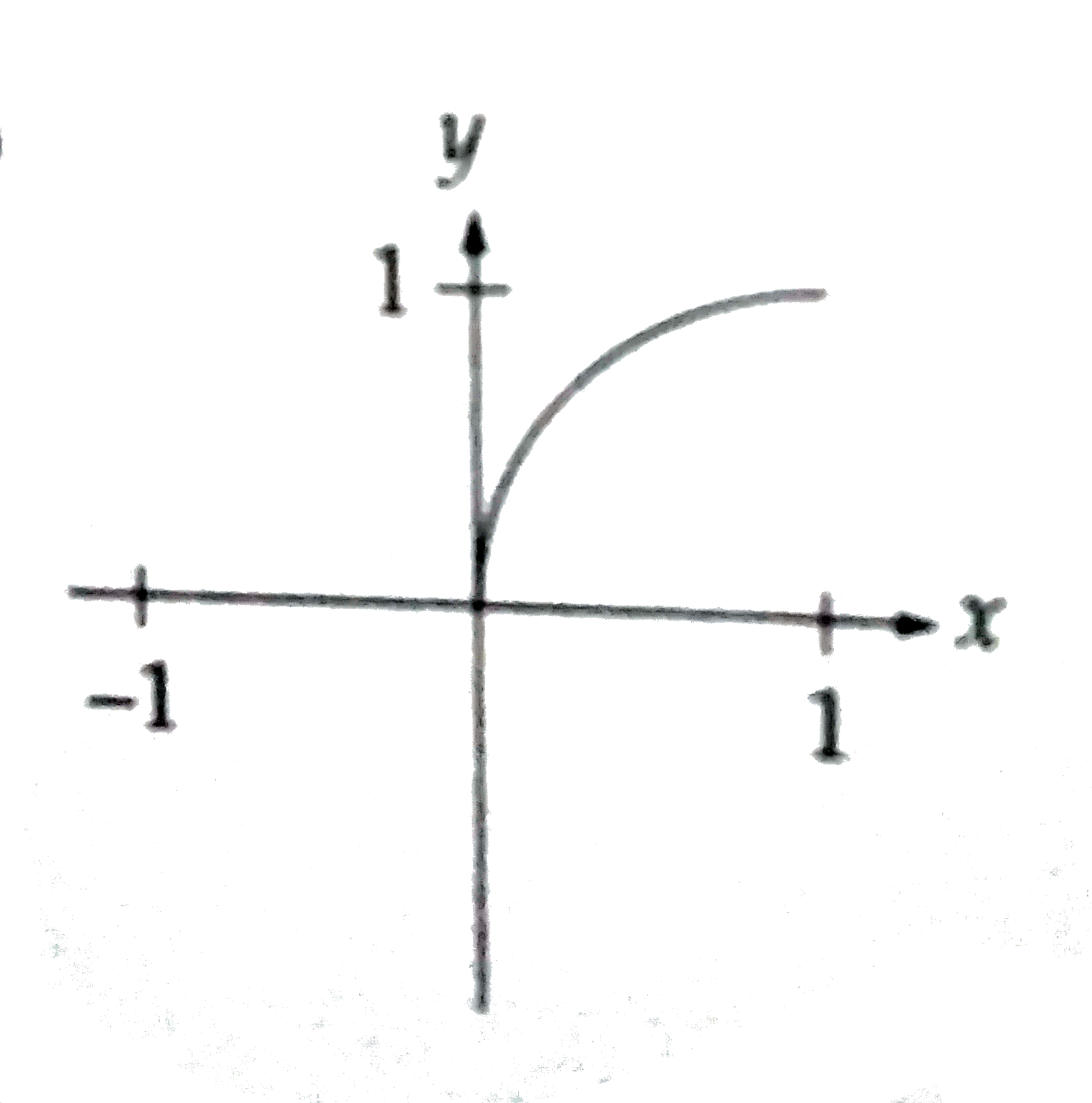 B
B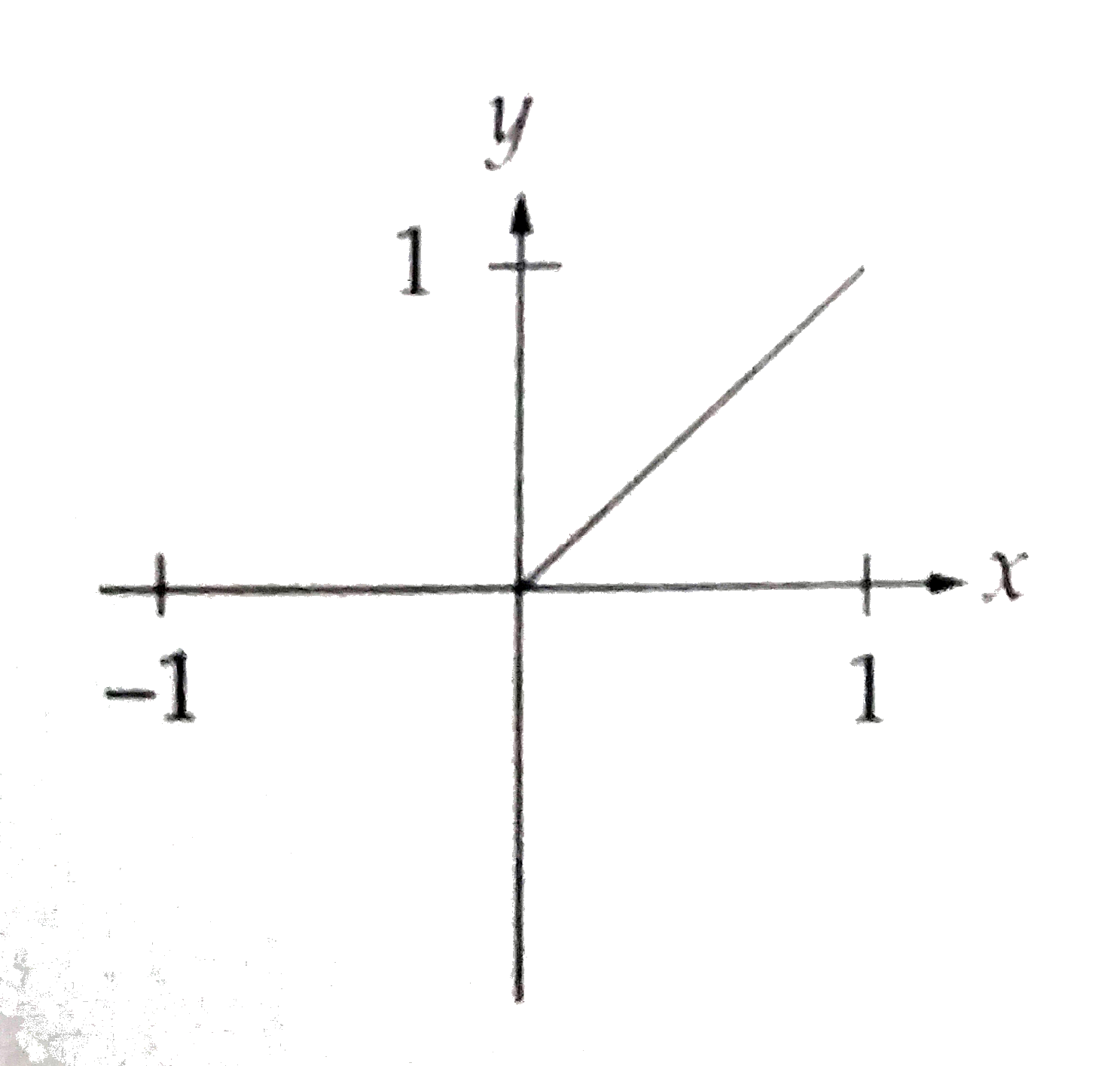 C
C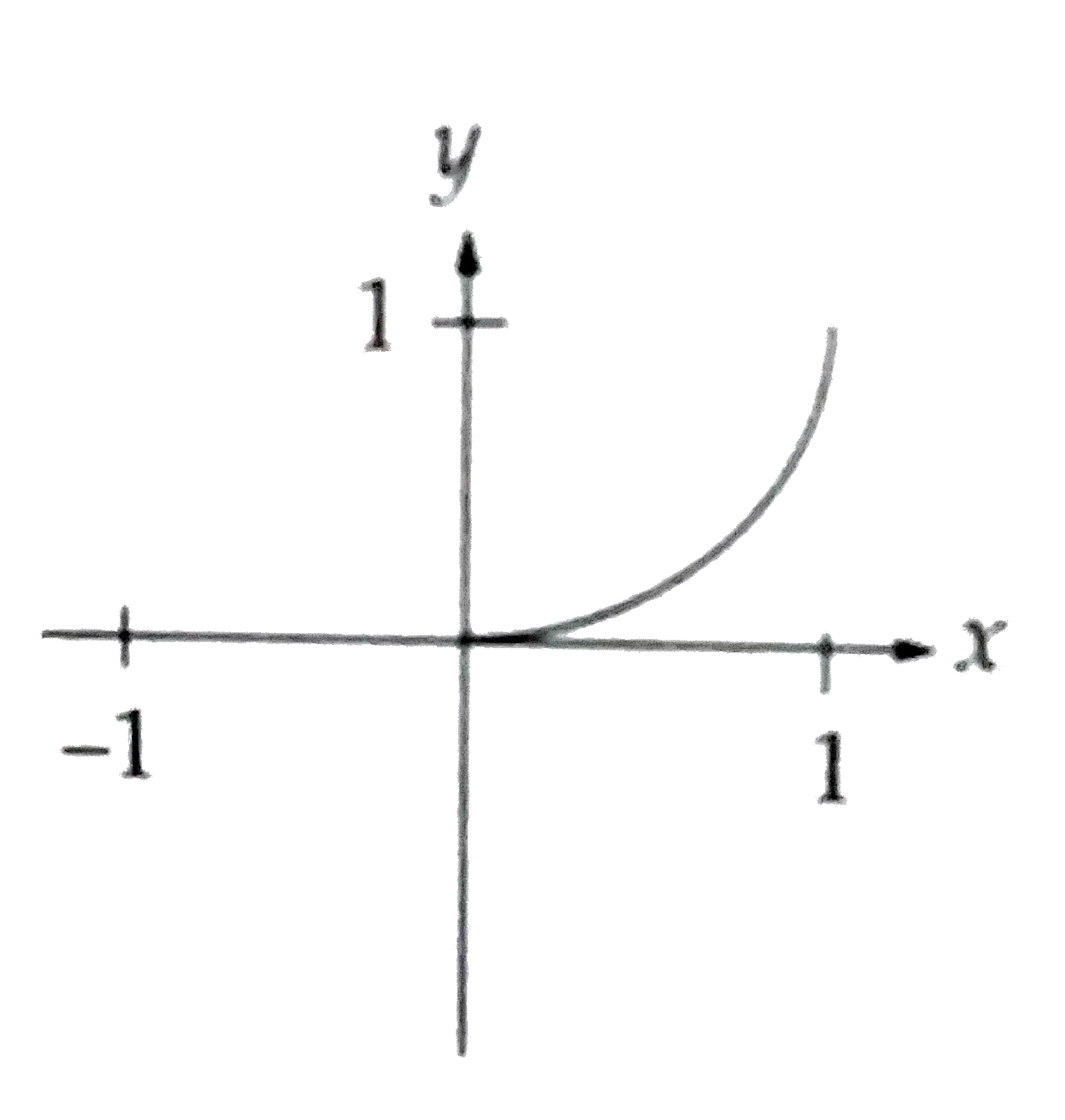 D
D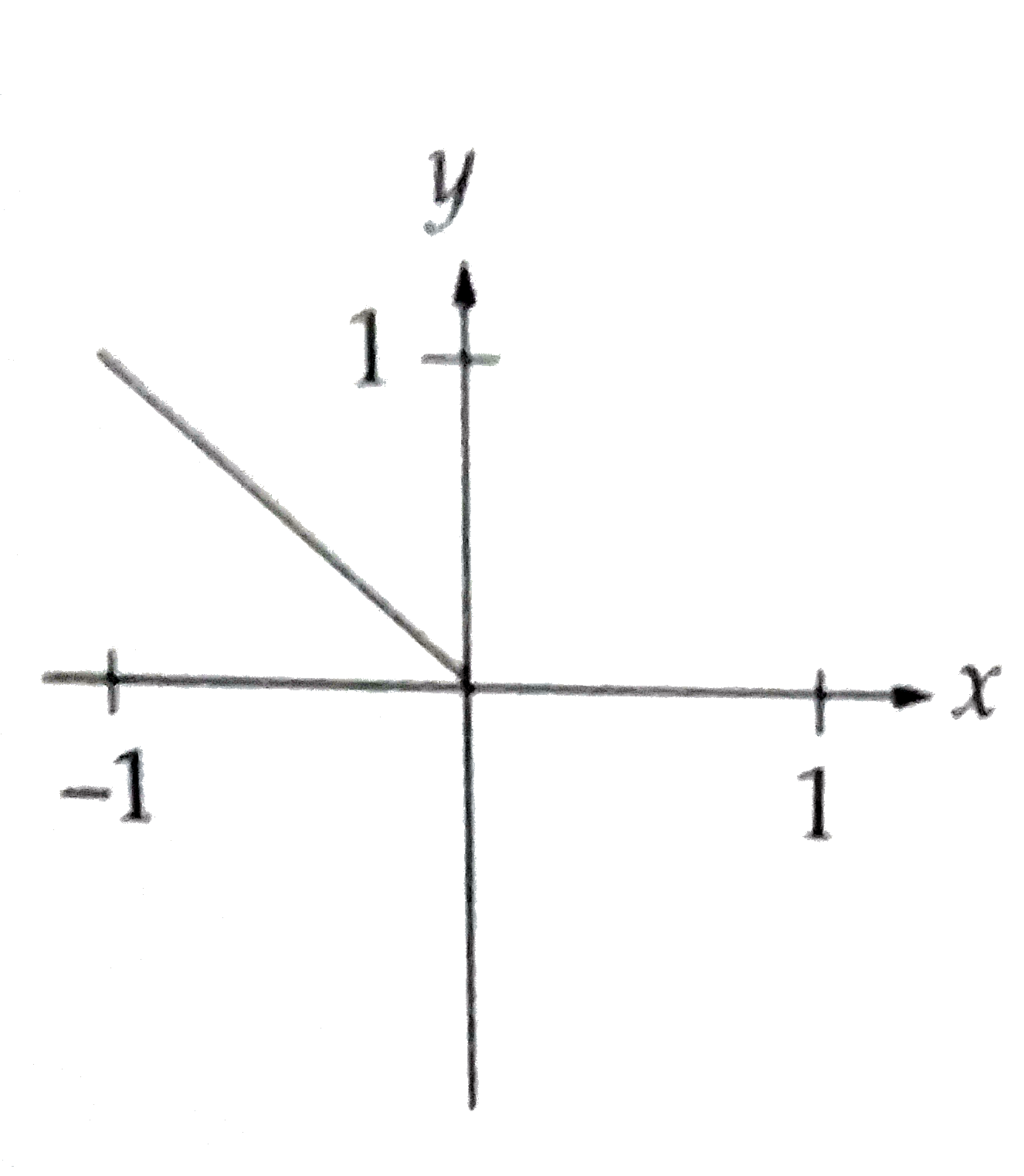
The mean annaul salary of an NBA player, S, can be estimated using the equation S=161,400(1.169)t, where S is measured in thousands of dollars, and t represents the number of yearts since 1980 for 0≤t≤20. Which of the following statements is the best interpretation of 161,400 in the context of this problem?
AThe estimated mean annual salary, in dollars, of an NBA player in 1980.BThe estimated mean annual salary, in dollars, of an NBA player in 2000.CThe estimated yearly increase in the mean annual salary of an NBA player.DThe estimated yearly decrease in the mean annual salary of an NBA player.
Form the differential equation of the family of curves represented c(y+c)2=x3,where is a parameter.
View SolutionFind the range of K for which the equation |z+i|−|z−i|=K represents a hyperbola.
View Solutionwhich of the following function corrtly represent the traveling wave equation for finite values of x and t ?
View SolutionThe equation x=t3+9 and y=3t34+6 represents a straight line where t is a parameter. Then y- intercept of the line is :
View SolutionWhen 6 is subtracted from 10p, the result is t. which of the following equation represent the statement above?
View Solution
