A, B and C represent switches in 'on' position and A', B' and C' represent them in 'off' position. Construct a switching circuit representing the polynomial ABC + AB'C + A'B'C. Using Boolean Algebra, prove that the given polynomial can be simplified to C (A + B'). Construct an equivalent switching circuit.
To solve the problem, we need to follow these steps:
Step 1: Construct the Switching Circuit
We start by constructing the switching circuit that represents the polynomial ABC+AB′C+A′B′C.
1. Identify the terms:
- The first term is ABC: This means all switches A, B, and C are ON.
- The second term is AB′C: This means switch A is ON, switch B is OFF, and switch C is ON.
- The third term is A′B′C: This means switch A is OFF, switch B is OFF, and switch C is ON.
2. Draw the circuit:
- Use AND gates for each of the terms:
- For ABC, connect A, B, and C to an AND gate.
- For AB′C, connect A, B' (NOT B), and C to another AND gate.
- For A′B′C, connect A' (NOT A), B' (NOT B), and C to another AND gate.
- Use an OR gate to combine the outputs of the three AND gates.
We start by constructing the switching circuit that represents the polynomial ABC+AB′C+A′B′C.
- The first term is ABC: This means all switches A, B, and C are ON.
- The second term is AB′C: This means switch A is ON, switch B is OFF, and switch C is ON.
- The third term is A′B′C: This means switch A is OFF, switch B is OFF, and switch C is ON.
- Use AND gates for each of the terms:
- For ABC, connect A, B, and C to an AND gate.
- For AB′C, connect A, B' (NOT B), and C to another AND gate.
- For A′B′C, connect A' (NOT A), B' (NOT B), and C to another AND gate.
- Use an OR gate to combine the outputs of the three AND gates.
Topper's Solved these Questions
- MATHEMATICS-2015BOOK - ICSECHAPTER - MATHEMATICS-2015EXERCISE - SECTION-B
6 Videos
- MATHEMATICS-2015BOOK - ICSECHAPTER - MATHEMATICS-2015EXERCISE - SECTION-C
5 Videos
- MATHEMATICS-2012BOOK - ICSECHAPTER - MATHEMATICS-2012EXERCISE - SECTION-C
6 Videos
- MATHEMATICS-2016BOOK - ICSECHAPTER - MATHEMATICS-2016EXERCISE - SECTION-C
6 Videos
Similar Questions
P,Q and R represent switches in on position and P',Q' and R' represent switches in off position. Construct a switching circuit representing the polynomial PR+Q(Q'+R)(P÷QR) . Using Boolean Algebra, simplify the polynomial expression and construct the simplified circuit
View SolutionWrite the Boolean function coresponding to the switching circuit given below:

A, B and C represent switches in 'on' position and A', B' and C' represent them in 'off' position. Using Boolean algebra, simplify the function and construct an equivalent switching circuit.
View Solution
Knowledge Check
In the circuit below, A and B represents two inputs and C represents the output . The circuit represents
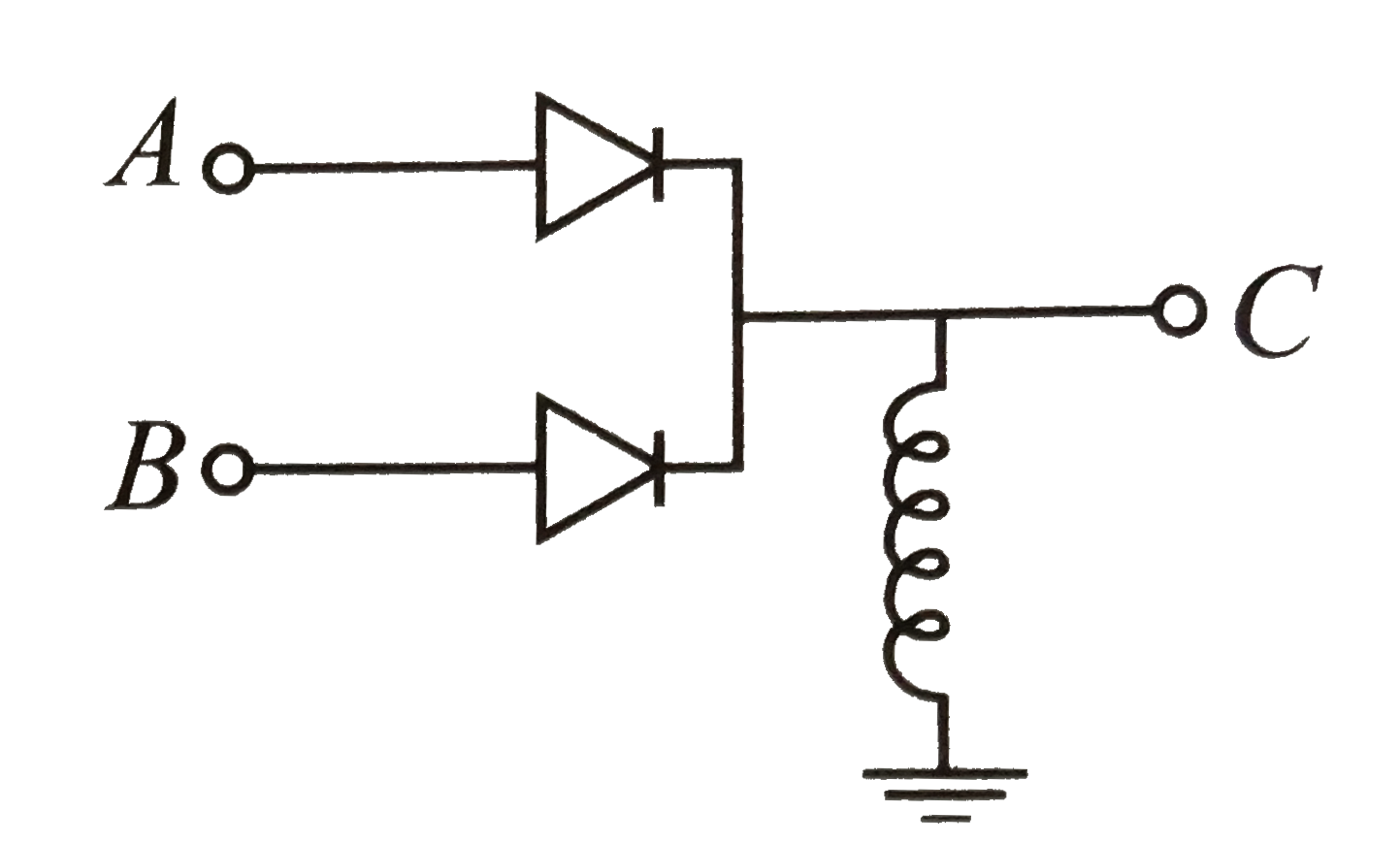 AAND gateBNOR gateCOR gateDNAND gate
AAND gateBNOR gateCOR gateDNAND gateIf a,b,and c are positive prime numbers , in the equation a-b=c, either b or c must represent which number ?
A13B11C7D5
Construct a circuit diagram for the following Boolean Function
(BC+A)(A'B'+C')+A'B'C'
Using laws of Boolean Algebra, simplify the function and draw the simplified circuit.
View SolutionIn the circuit below, A and B represents two inputs and C represents the output, the circuit represents.
 .
.
View SolutionIn the circuit below, A and B represent two inputs and C represents the output.
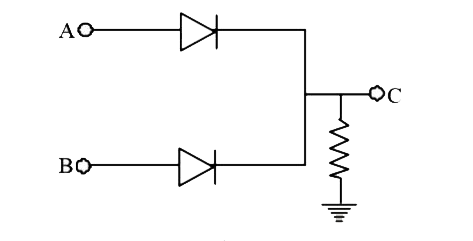
The circuit represents
View SolutionIf A=3B = 5C, find A:B:C.
View SolutionIf A,B and C are the elements of Boolean algebra, simplify the expression (A'+B') (A+C')+B' (B+C). Draw the simplified circuit.
View SolutionCondsider
 .
.
In the circuit shown is the switch can be shifted to positions 1 and 2 The charge on capacitor C1 when the switch is at position 1 is.
View Solution
