In the following figure :
AD⊥BC,AC=26,CD=10,BC=42,∠DAC=xand∠B=y.
Find the value of :
(i) cot x
(ii) 1sin2y−1tan2y
(iii) 6cosx−5cosy+8tany
The correct Answer is:(i) 225
(ii) 1
(iii) 614
To solve the given problem step by step, we will break it down into three parts as specified in the question.
Given:
- AC = 26
- CD = 10
- BC = 42
- Angle DAC = x
- Angle B = y
Step 1: Finding cot x
1. Identify the triangle ADC:
- In triangle ADC, AD is perpendicular to BC.
- We know AC (hypotenuse) = 26 and CD (perpendicular) = 10.
2. Calculate the length of AD using Pythagoras theorem:
- According to the Pythagorean theorem:
AC2=AD2+CD2
- Plugging in the values:
262=AD2+102
676=AD2+100
AD2=676−100=576
AD=√576=24
3. Calculate cot x:
- Cotangent is defined as the adjacent side over the opposite side.
- In triangle ADC, cot x = AD/CD.
- Thus,
cotx=ADCD=2410=2.4
Step 2: Finding 1sin2y−1tan2y
1. Identify triangle ADB:
- In triangle ADB, we have:
- AD = 24 (perpendicular)
- BD = BC - CD = 42 - 10 = 32 (base)
2. Calculate AB using Pythagorean theorem:
- Using the Pythagorean theorem:
AB2=AD2+BD2
- Plugging in the values:
AB2=242+322=576+1024=1600
AB=√1600=40
3. Calculate siny and tany:
- siny=ADAB=2440=35
- tany=ADBD=2432=34
4. Calculate 1sin2y−1tan2y:
- sin2y=(35)2=925
- tan2y=(34)2=916
- Thus,
1sin2y=259,1tan2y=169
- Therefore,
1sin2y−1tan2y=259−169=99=1
Step 3: Finding 6cosx−5cosy+8tany
1. Calculate cosx and cosy:
- For cosx:
cosx=ADAC=2426=1213
- For cosy:
cosy=BDAB=3240=45
2. Substituting values into the expression:
- Calculate 6cosx:
6cosx=61213=6⋅1312=7812=6.5
- Calculate 5cosy:
5cosy=545=5⋅54=254=6.25
- Calculate 8tany:
8tany=8⋅34=6
3. Final calculation:
- Combine all parts:
6cosx−5cosy+8tany=6.5−6.25+6=6.25+6=12.25
Final Answers:
(i) cotx=2.4
(ii) 1sin2y−1tan2y=1
(iii) 6cosx−5cosy+8tany=12.25
- AC = 26
- CD = 10
- BC = 42
- Angle DAC = x
- Angle B = y
- In triangle ADC, AD is perpendicular to BC.
- We know AC (hypotenuse) = 26 and CD (perpendicular) = 10.
- According to the Pythagorean theorem:
AC2=AD2+CD2
- Plugging in the values:
262=AD2+102
676=AD2+100
AD2=676−100=576
AD=√576=24
- Cotangent is defined as the adjacent side over the opposite side.
- In triangle ADC, cot x = AD/CD.
- Thus,
cotx=ADCD=2410=2.4
- In triangle ADB, we have:
- AD = 24 (perpendicular)
- BD = BC - CD = 42 - 10 = 32 (base)
- Using the Pythagorean theorem:
AB2=AD2+BD2
- Plugging in the values:
AB2=242+322=576+1024=1600
AB=√1600=40
- siny=ADAB=2440=35
- tany=ADBD=2432=34
- sin2y=(35)2=925
- tan2y=(34)2=916
- Thus,
1sin2y=259,1tan2y=169
- Therefore,
1sin2y−1tan2y=259−169=99=1
- For cosx:
cosx=ADAC=2426=1213
- For cosy:
cosy=BDAB=3240=45
- Calculate 6cosx:
6cosx=61213=6⋅1312=7812=6.5
- Calculate 5cosy:
5cosy=545=5⋅54=254=6.25
- Calculate 8tany:
8tany=8⋅34=6
- Combine all parts:
6cosx−5cosy+8tany=6.5−6.25+6=6.25+6=12.25
(i) cotx=2.4
(ii) 1sin2y−1tan2y=1
(iii) 6cosx−5cosy+8tany=12.25
Topper's Solved these Questions
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (3 MARKS QUESTIONS )
9 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (4 MARKS QUESTIONS )
8 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )
4 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)
118 Videos
Similar Questions
Find the value of tan−1(xy)−tan−1(x−yx+y)
View SolutionFind the value of tan−1(xy)−tan−1(x−yx+y)
View SolutionFind the value of tan−1(xy)−tan−1(x−yx+y)
View SolutionFind the value of
tan{12sin−1(2x1+x2)+12cos−1(1−y21+y2)}
View SolutionProve that : sinx−sinycosx+cosy=tan(x−y2)
View SolutionProve that : sinx+sinycosx+cosy=tan(x+y2)
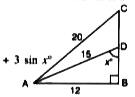
View SolutionIn the given figure ∠B=90∘and∠ADB=x∘, Find :
(i) sin∠CAB
(ii)cos2C∘+sin2C∘
(iii) tanx∘−cosx∘+3sinx∘
View SolutionIf x+y+z=xyzandx,y,z>0, then find the value of tan−1x+tan−1y+tan−1z
View SolutionFrom the given figure, find :
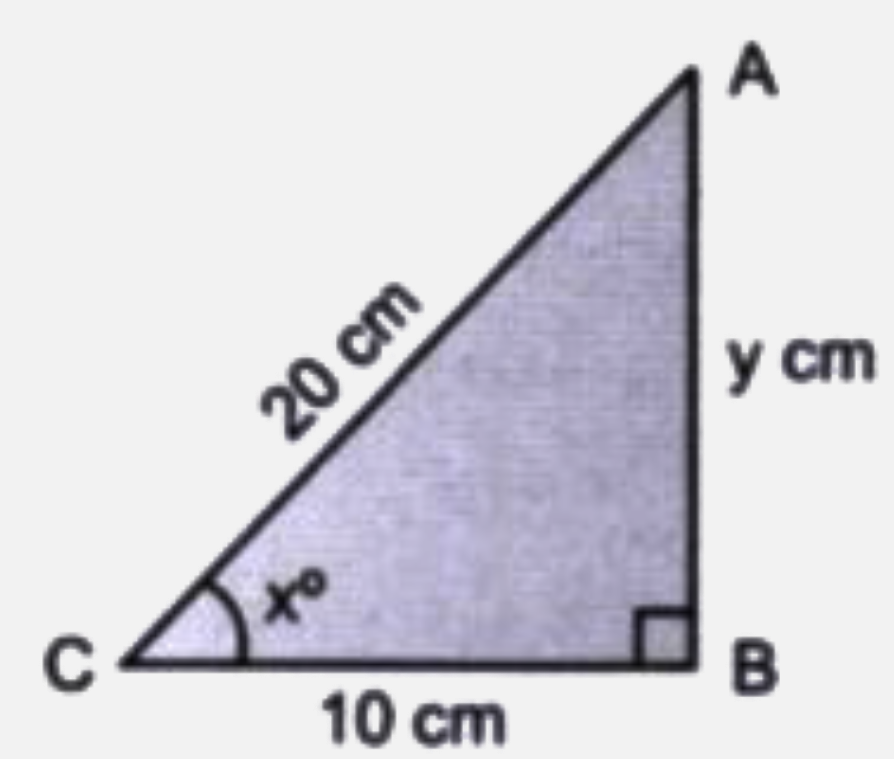
(i) cosx∘
(ii) x∘
(iii) 1tan2x∘−1sin2x∘
(iv) use tanx∘, to find the value of y
View SolutionIf x>y>0, then find the value of tan−1.xy+tan−1[x+yx−y]
View Solution
