An ultrasonic wave is sent from a ship towards the bottom of the sea. It is found that the time interval between the sending and the receiving of the wave is 1.5 s. Calculate the depth of the sea, , if the velocity of sound in sea water is 1400ms−1.
To solve the problem of finding the depth of the sea using the given information about the ultrasonic wave, we can follow these steps:
Step 1: Understand the relationship between distance, speed, and time
The basic formula that relates speed (V), distance (D), and time (t) is:
V=Dt
In this case, the distance we are interested in is the depth of the sea (D), but since the ultrasonic wave travels to the bottom of the sea and back to the ship, the total distance traveled is twice the depth.
Step 2: Set up the equation for the total distance
Since the wave travels to the bottom and back, the total distance (D_total) is:
Dtotal=2×D
Thus, we can rewrite the speed formula as:
V=2Dt
Step 3: Rearrange the formula to find the depth
We can rearrange the formula to solve for depth (D):
D=V×t2
Step 4: Substitute the known values
From the problem, we know:
- The speed of sound in seawater (V) = 1400 m/s
- The time interval (t) = 1.5 s
Substituting these values into the equation:
D=1400m/s×1.5s2
Step 5: Calculate the depth
Now, we perform the calculation:
1. Calculate 1400×1.5:
1400×1.5=2100
2. Now divide by 2:
D=21002=1050m
Final Answer
The depth of the sea is:
D=1050meters
---
The basic formula that relates speed (V), distance (D), and time (t) is:
V=Dt
In this case, the distance we are interested in is the depth of the sea (D), but since the ultrasonic wave travels to the bottom of the sea and back to the ship, the total distance traveled is twice the depth.
Since the wave travels to the bottom and back, the total distance (D_total) is:
Dtotal=2×D
Thus, we can rewrite the speed formula as:
V=2Dt
We can rearrange the formula to solve for depth (D):
D=V×t2
From the problem, we know:
- The speed of sound in seawater (V) = 1400 m/s
- The time interval (t) = 1.5 s
D=1400m/s×1.5s2
Now, we perform the calculation:
1. Calculate 1400×1.5:
1400×1.5=2100
2. Now divide by 2:
D=21002=1050m
The depth of the sea is:
D=1050meters
Topper's Solved these Questions
Similar Questions
A ship on the surface of water sends a signal and receives it back from a submarine inside water after 4 s. Calculate the distance of the submarine from the ship. (The speed of sound in water is 1450 m s−1).
View SolutionThe figure shows the snapshot of a sound wave in a certain medium at a certain instant.
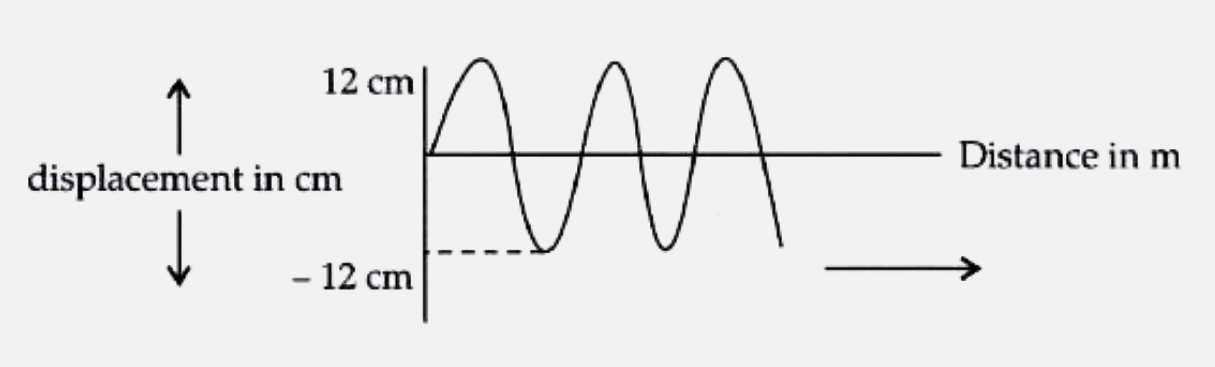
If the velocity of the wave is 4ms−1 , calculate the wavelength of the wave if its frequency is 20 Hz.
View SolutionAn observer stands at a certain distance away from a cliff and produces a loud sound. He hears the echo of the sound after 1.8 s. Calculate the distance between the cliff and the observer if the velocity of sound in air is 340ms−1.
View SolutionThe speed of sound in water is 1500 m/s. A boat man hears an echo 3 s after sending a sound pulse into the sea. What is the depth of the sea?
View SolutionA sound wave travelling in water has wavelength 0.4 m.
Is this wave audible in air ? (The speed of sound in water = 1400ms−1)
View SolutionMicrowaves are reflected from a distant airplane approaching a stationary observer. It is found that when the reflected waves beat against the waves radiating from the source, the beat frequency is 900 Hz. Calculate the approach speed of the airplane if the wavelength of the microwave is 0.1 H. Velocity of microwave is 3×108 m/s.
View SolutionThe speed of sound in water is 1600 m/s. A boat man hears an echo 3 s after sending an ultrasonic sound into the sea. What is the depth of the sea?
View SolutionA man standing between two cliffs produces a sound and hears two successive echoes at intervals of 3 s and 4 s respectively. Calculate the distance between the two cliffs.
The speed of sound in the air is 330ms−1.
View SolutionThe time interval between a lightning flash and the first sound of thunder is 5 s. If the speed of sound in air is 330 m s−1, find the distance of flash from the observer.
View SolutionIn a SONAR, ultrasonic waves are sent into the sea water and the reflected waves from a sunken ship are received after 2.0 s. If the velocity of waves in sea water is 1450 m s−1 , find the depth of the sunken ship.
View Solution
