Write True or False C(x)=∫MCdx+c
To determine whether the statement C(x)=∫MCdx+c is true or false, we can analyze the components involved in the equation.
1. Understanding the Functions:
- C(x) represents the total cost function.
- MC represents the marginal cost function, which is the derivative of the total cost function with respect to x.
2. Relating Marginal Cost to Total Cost:
- By definition, the marginal cost function MC is given by:
MC=dCdx
- This means that the marginal cost is the rate of change of the total cost function.
3. Integrating the Marginal Cost:
- To find the total cost function C(x) from the marginal cost MC, we can integrate MC:
C(x)=∫MCdx+c
- Here, c is the constant of integration, which represents fixed costs or initial costs when x=0.
4. Conclusion:
- Since we have established that the total cost function can indeed be expressed as the integral of the marginal cost function plus a constant, the statement C(x)=∫MCdx+c is True.
Final Answer:
True
- C(x) represents the total cost function.
- MC represents the marginal cost function, which is the derivative of the total cost function with respect to x.
- By definition, the marginal cost function MC is given by:
MC=dCdx
- This means that the marginal cost is the rate of change of the total cost function.
- To find the total cost function C(x) from the marginal cost MC, we can integrate MC:
C(x)=∫MCdx+c
- Here, c is the constant of integration, which represents fixed costs or initial costs when x=0.
- Since we have established that the total cost function can indeed be expressed as the integral of the marginal cost function plus a constant, the statement C(x)=∫MCdx+c is True.
True
Topper's Solved these Questions
Similar Questions
Write a value of ∫eaxsinbx dx
View SolutionWrite true or false for the following statements:
Steam at100∘C causes more severe burns than water at 100∘C _________.
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
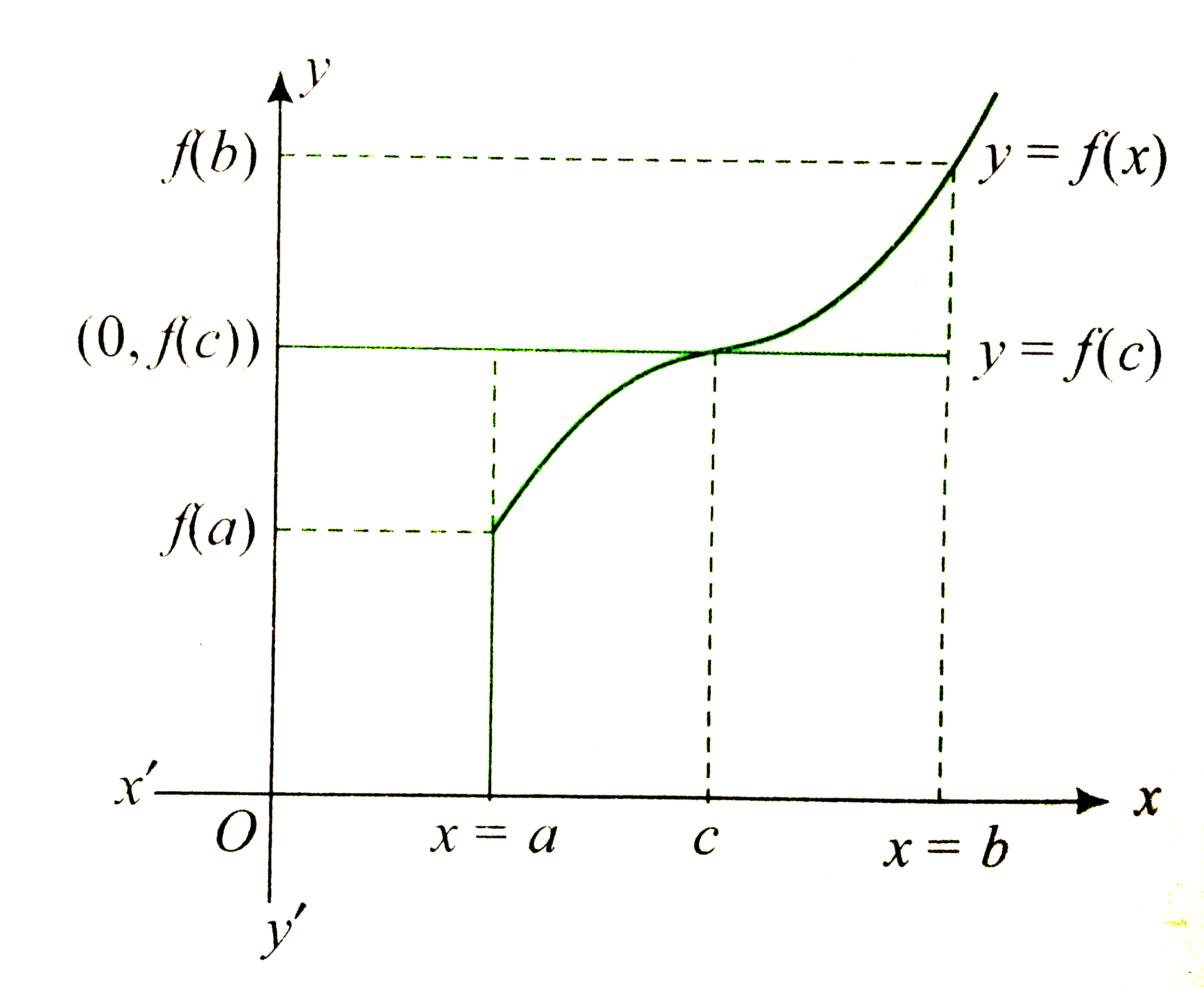
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
View SolutionWrite T for True and F for the False. Correct the false statement
The formula for calculating area is length x breadth for rectangle.
View SolutionWrite a value of ∫eaxcosbx dx
View SolutionAnswer in true or false:
(a+b)×(a+c)=a+(b+c)
View SolutionWrite a value of ∫(logx)nx dx
View SolutionWrite a value of ∫ax3+ax dx
View SolutionWrite the value of ∫dxx2+16
View SolutionRead the following statements about cancer . Identify the true and false ones and select the correct option .
A . Cancer cells lose the property of contact inhibition
B. The property of metastasis is mostly found in benign tumors .
C. The transformation of normal cells into cancerous cells occurs only because of chemical agents.
D. The chemical carcinogen present in tobacco smoke is a major cause of lung cancer.
(a) A - True , B - False , C - False , D - True
(b) A - False , B - True , C - True , D - False
(c) A - True , B - False , C - True , D - False
(d) A - False , B - True , C - False , D - True
View Solution
