A firm starts producing pocket calculators. During the first year, the cost for setting up the unit is 3 lakh. The additional cost of producing a calculator is Rs 70. This cost is directly related to the production and the variable cost. The firm expects the revenue from the sales of the calculators to be 270 per calculator. Assuming all the produced calculators are sold, find the number x of the calculators for which
(i) the firm will breakeven
(ii) will make profit
(iii) will suffer a loss.
To solve the problem, we need to analyze the cost and revenue functions for the firm producing pocket calculators.
Step 1: Define the Cost Function
The total cost (C) of producing x calculators consists of a fixed setup cost and a variable cost per calculator.
- Fixed cost = Rs 3,00,000 (3 lakh)
- Variable cost per calculator = Rs 70
Thus, the cost function can be expressed as:
C(x)=300000+70x
Step 2: Define the Revenue Function
The revenue (R) generated from selling x calculators is given by the price per calculator multiplied by the number of calculators sold.
- Revenue per calculator = Rs 270
Thus, the revenue function can be expressed as:
R(x)=270x
Step 3: Determine the Break-Even Point
The break-even point occurs when total revenue equals total cost, i.e., when profit is zero. We set the revenue function equal to the cost function:
R(x)=C(x)
270x=300000+70x
Now, we solve for x:
1. Subtract 70x from both sides:
270x−70x=300000
200x=300000
2. Divide both sides by 200:
x=300000200
x=1500
Thus, the firm will break even when it sells 1500 calculators.
Step 4: Determine When the Firm Will Make a Profit
The firm will make a profit when the revenue is greater than the cost:
R(x)>C(x)
This implies:
270x>300000+70x
Subtract 70x from both sides:
200x>300000
Dividing both sides by 200 gives:
x>1500
Thus, the firm will make a profit when it sells more than 1500 calculators.
Step 5: Determine When the Firm Will Suffer a Loss
The firm will suffer a loss when the revenue is less than the cost:
R(x)<C(x)
This implies:
270x<300000+70x
Subtract 70x from both sides:
200x<300000
Dividing both sides by 200 gives:
x<1500
Thus, the firm will suffer a loss when it sells fewer than 1500 calculators.
Summary of Results
1. The firm will break even when it sells 1500 calculators.
2. The firm will make a profit when it sells more than 1500 calculators.
3. The firm will suffer a loss when it sells fewer than 1500 calculators.
The total cost (C) of producing x calculators consists of a fixed setup cost and a variable cost per calculator.
- Variable cost per calculator = Rs 70
C(x)=300000+70x
The revenue (R) generated from selling x calculators is given by the price per calculator multiplied by the number of calculators sold.
R(x)=270x
The break-even point occurs when total revenue equals total cost, i.e., when profit is zero. We set the revenue function equal to the cost function:
270x=300000+70x
1. Subtract 70x from both sides:
270x−70x=300000
200x=300000
x=300000200
x=1500
The firm will make a profit when the revenue is greater than the cost:
R(x)>C(x)
This implies:
270x>300000+70x
200x>300000
x>1500
The firm will suffer a loss when the revenue is less than the cost:
R(x)<C(x)
This implies:
270x<300000+70x
200x<300000
x<1500
1. The firm will break even when it sells 1500 calculators.
2. The firm will make a profit when it sells more than 1500 calculators.
3. The firm will suffer a loss when it sells fewer than 1500 calculators.
Topper's Solved these Questions
Similar Questions
Knowledge Check
For manufacturing a certain item, the fixed cost is 9000 and the variable cost of producing each unit is Rs 30. The average cost of producing 60 units is -
ARs 150BRs 180CRs 240DRs 120The cost of sales promotion per unit is
ALowBHighCAt parDNoneThe cost of production of a certain instrument is directly proportional to the number of units produced. The cost of production for 300 units is $300. What is the cost of production for 270 units?
A270B300C325D370
The marginal cost of a product is given by MC = 2x + 30 and the fixed cost is Rs. 120. Find
(i) the total cost of producing 100 units.
(ii) the cost of increasing output from 100 to 200 units.
View SolutionThe cost of 213 metres of cloth is Rs 7514. Find its cost per metre.
View SolutionCalculate the cost of living index number from the following group data:
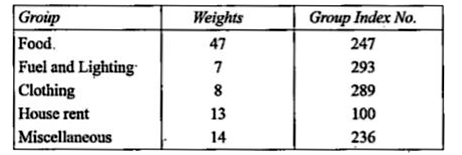
View SolutionCalculate the cost of living index for the following data:

View SolutionIf the total cost of producing x units of a commodity is given by C(x)=13x2+x2−15x+300, then the marginal cost when x=5 is
View Solution