In the circuit, given figure below the length of the wire AB = 400 cm. Where should the jockey J be placed, so that the galvanometer shows a zero deflection?
To find the position where the jockey J should be placed so that the galvanometer shows zero deflection, we can use the principle of a Wheatstone bridge. Here's a step-by-step solution:
Step 1: Understand the Circuit
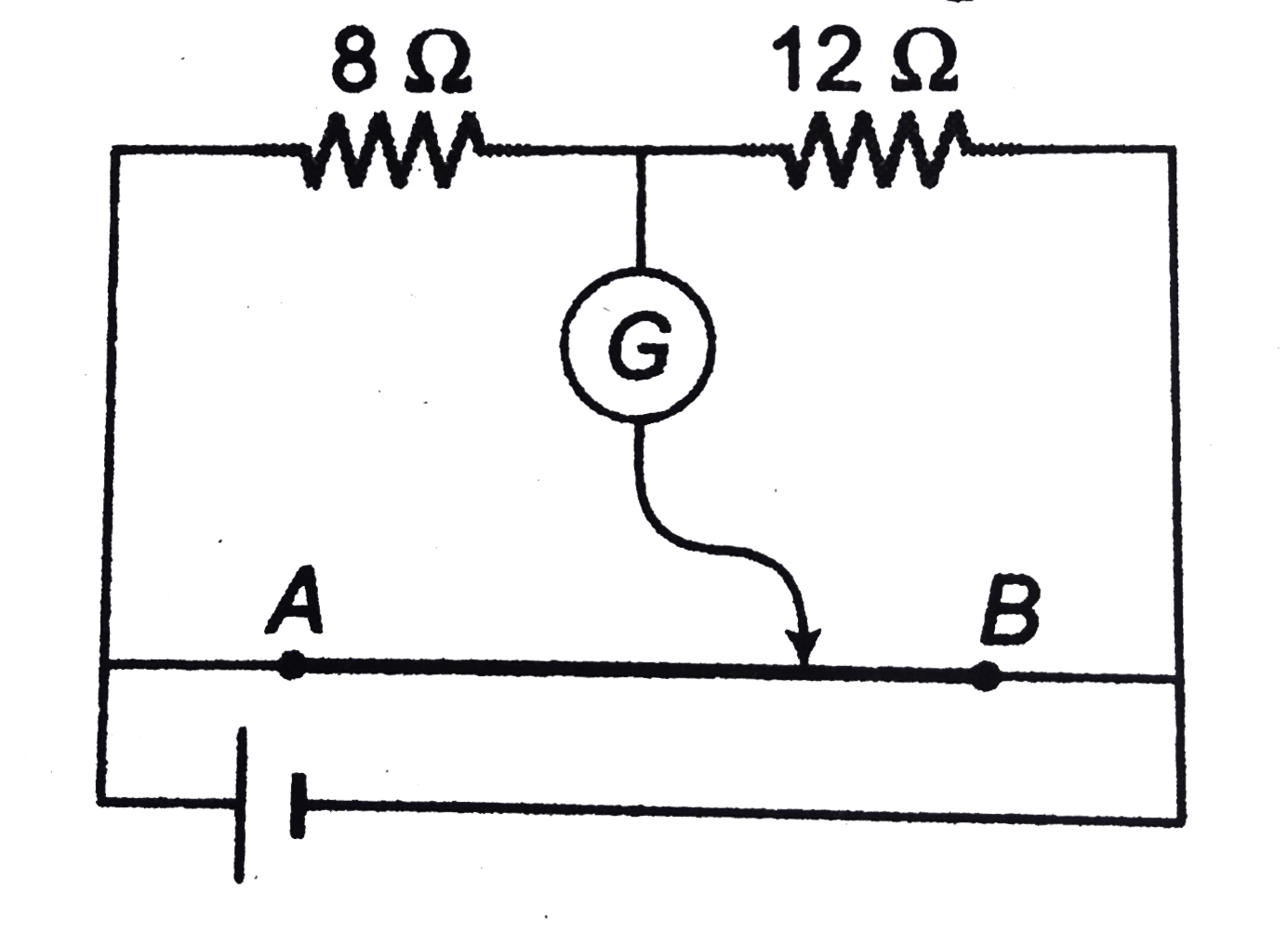
In the given circuit, we have two resistors: R1 = 8 ohms and R2 = 12 ohms. The total length of the wire AB is 400 cm. We need to find the position of the jockey J along the wire AB where the galvanometer shows zero deflection.
Step 2: Set Up the Proportions
When the galvanometer shows zero deflection, it indicates that the potential difference across it is zero. This condition can be expressed using the ratio of the resistances and the lengths of the wire segments:
R1R2=x400−x
Where:
- R1=8 ohms (resistor connected to one end of the wire)
- R2=12 ohms (resistor connected to the other end of the wire)
- x = distance from point A to the jockey J
- 400−x = distance from point J to point B
Step 3: Substitute the Values
Substituting the values of R1 and R2 into the equation:
812=x400−x
Step 4: Simplify the Equation
We can simplify the left side:
23=x400−x
Step 5: Cross-Multiply
Cross-multiplying gives us:
2(400−x)=3x
Step 6: Expand and Rearrange
Expanding the left side:
800−2x=3x
Now, rearranging the equation:
800=3x+2x
800=5x
Step 7: Solve for x
Now, divide both sides by 5:
x=8005=160 cm
Conclusion
Thus, the jockey J should be placed at 160 cm from point A along the wire AB for the galvanometer to show zero deflection.
---
In the given circuit, we have two resistors: R1 = 8 ohms and R2 = 12 ohms. The total length of the wire AB is 400 cm. We need to find the position of the jockey J along the wire AB where the galvanometer shows zero deflection.
When the galvanometer shows zero deflection, it indicates that the potential difference across it is zero. This condition can be expressed using the ratio of the resistances and the lengths of the wire segments:
- R1=8 ohms (resistor connected to one end of the wire)
- R2=12 ohms (resistor connected to the other end of the wire)
- x = distance from point A to the jockey J
- 400−x = distance from point J to point B
Substituting the values of R1 and R2 into the equation:
We can simplify the left side:
Cross-multiplying gives us:
Expanding the left side:
Now, divide both sides by 5:
Thus, the jockey J should be placed at 160 cm from point A along the wire AB for the galvanometer to show zero deflection.
Similar Questions
The potentiometer wire AB shown in figure is 40 cm long. Where should the free end of the galvanometer be connected on AB so that the galvanometer may show zero deflection?

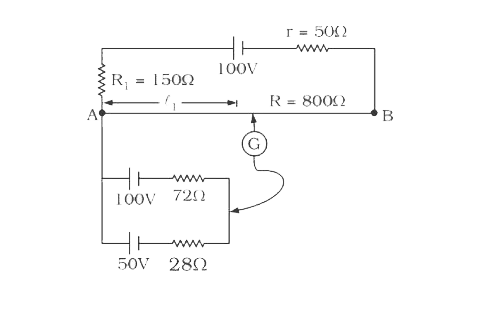
View SolutionIn the circuit shown, the length of AB is 100 cm. The lengthj1 for which the galvanometer shows zero deflection is __________ cm.
View SolutionThe potentiometer wire AB shown in figure is 40cm long. Where the free end of the galvanometer should be connected on AB so that the galvanometer may show zero deflection?
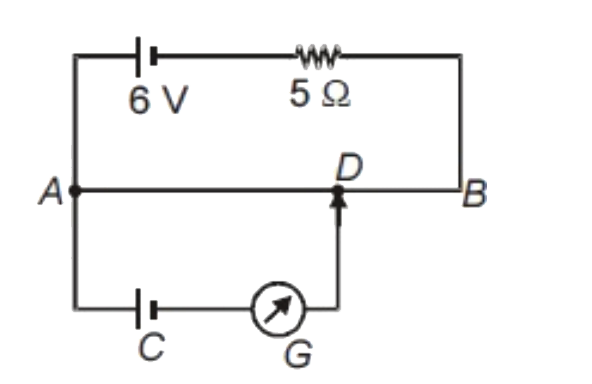
View SolutionIn the potentiometer circuit shown in the figure the internal resistance of the 6V battery is 1Ω and length of the wire AB is 100 cm . When AD = 60 cm , the galvanometer shows no deflection . The EMF of the cell C is (the resistance of the wire AB is 2Ω )
View SolutionFor the potentiometer arrangement shown in the figure, length of wire AB is 100 cm and its resistance is 9Ω. Find the length AC for which the galvanometer G will show zero deflection.
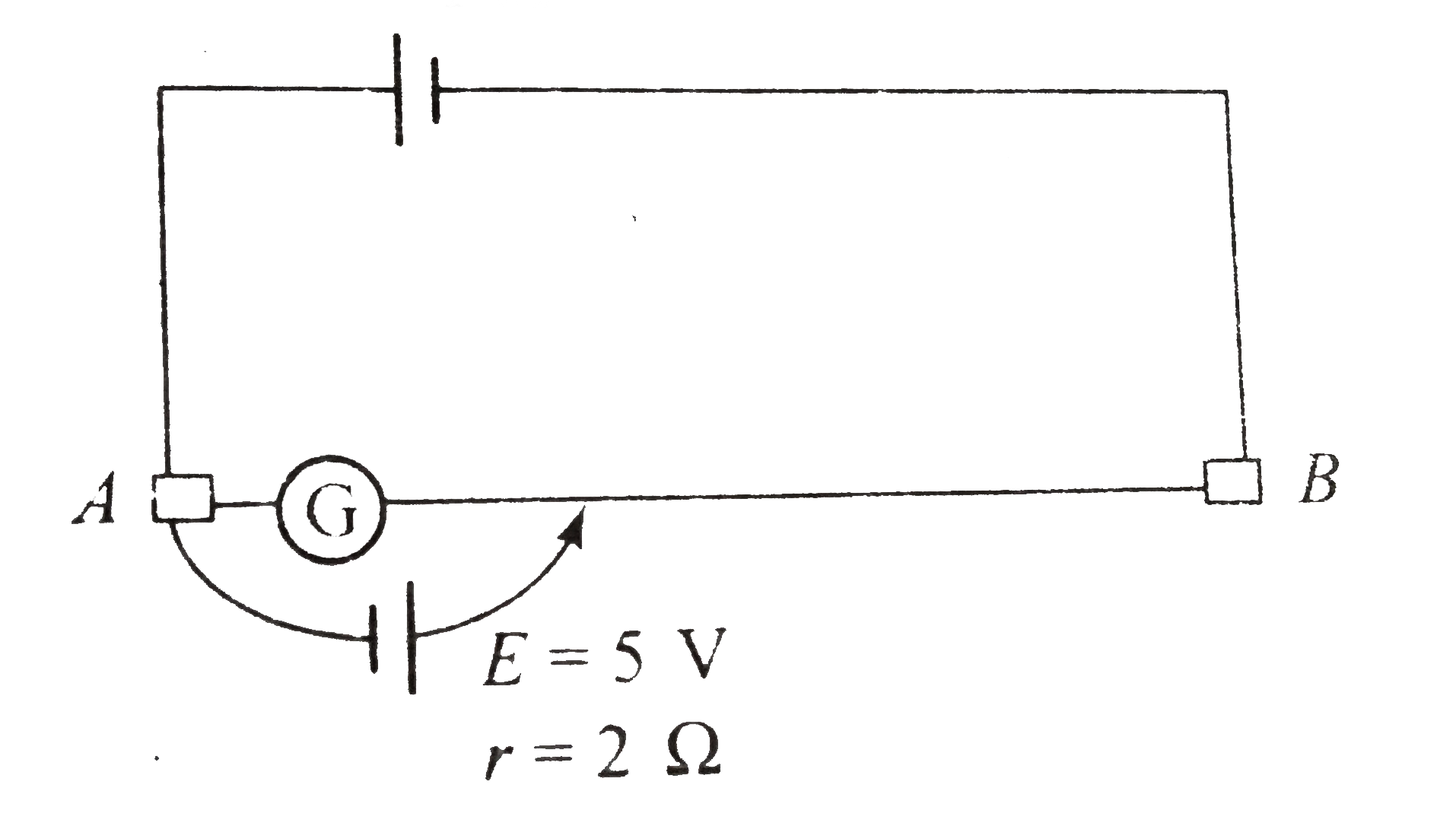
View SolutionConsider the potentiometer circuit arranged as in figure. The potentiometer wire is 600cm long. At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? b) If the jockey touches the wire at a distance of 560cm from A, What will be the current in the galvanometer?
View SolutionIn the adjacent circuit a resisttance R is used. Initially with 'wire AB' not in the circuit, the galavanometer shhows a deflection of d divisions. Now, the wire AB is conneted parallel to the galvanometer and the galvanometer shows a deflection defiction nearly d/2 divisions. Therefore
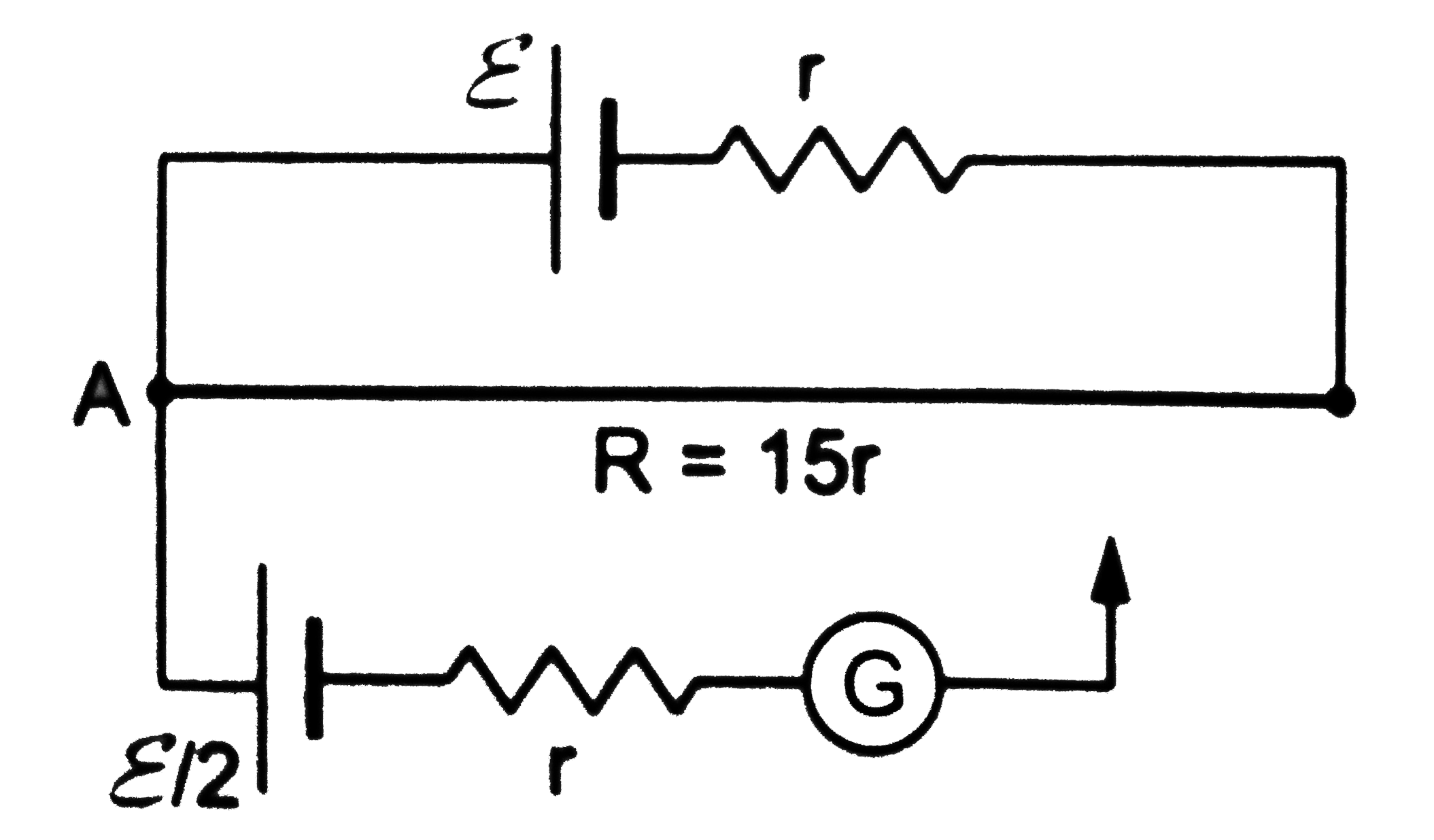
View SolutionThe potentiometer wire AB is 600 cm long . At what distance (in cm) from A should the jockey J touch the wire to get zero deflection in the galvanometer?
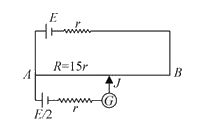
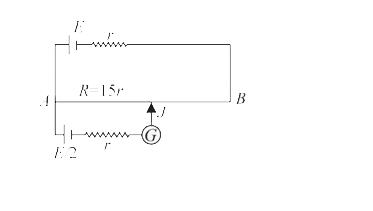
View SolutionThe potentiometer wire AB is 600cm long. At what distance (in cm) from A should the jockey J touch the wire to get zero deflection in the galvanometer?
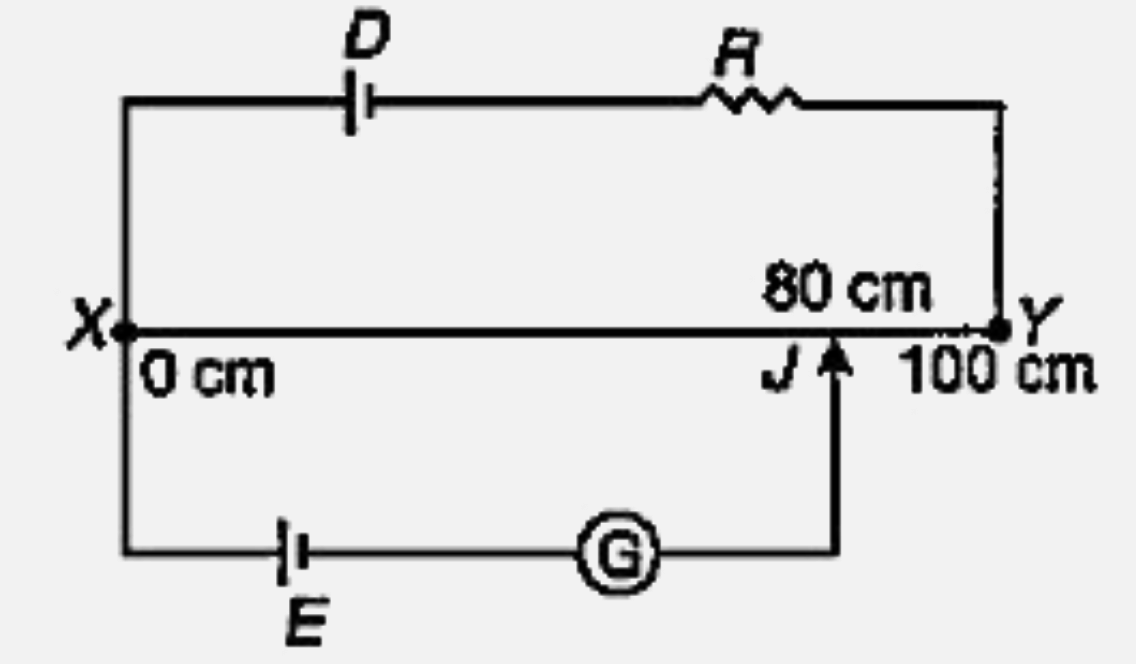
View SolutionFigure alongside shows a uniform manganin wire XY of length 100 cm and resistance 9Ω, connected to an accumulator D of emf 4 V and internal resistance 1Ω through a variable resistance R. E is a cell of emf 1.8 V connected to the wire XY via a jockey J and a central zero galvanometer G. It is found that the galvanometer shows no deflection when XJ = 80 cm. Find the value of R.
View Solution
