A ray LM of monochromatic light incident normally on one refracting surface AB of a regular glass prism ABC emerges in air from the adjacent surface C as shown in figure. Calculate the refractive index of the material of the prism.
To calculate the refractive index of the material of the prism, we can follow these steps:
Step 1: Understand the Geometry of the Prism
We have a regular glass prism ABC with a ray LM of monochromatic light incident normally on surface AB. The angle of the prism (angle A) is given as 60 degrees.
Step 2: Identify the Angles
Since the ray LM is incident normally on surface AB, it will not bend at this surface. When it reaches the surface AC, it forms an angle of 60 degrees with the normal. Therefore, the angle MNP (the angle of refraction at surface AC) is also 60 degrees.
Step 3: Apply Snell's Law
At the surface AC, we can apply Snell's law, which states:
n1sin(θ1)=n2sin(θ2)
Where:
- n1 is the refractive index of air (approximately 1),
- θ1 is the angle of incidence (which is 60 degrees),
- n2 is the refractive index of the prism (which we need to find),
- θ2 is the angle of refraction (which is also 60 degrees).
Step 4: Substitute the Values into Snell's Law
Substituting the known values into Snell's law:
1⋅sin(60∘)=n2⋅sin(60∘)
Step 5: Simplify the Equation
Since sin(60∘) is common on both sides, we can simplify:
1=n2
Step 6: Find the Refractive Index
From the equation, we can see that:
n2=1
However, we need to consider the geometry of the prism. The refractive index of the prism material can also be calculated using the formula:
μ=1sin(A/2)
where A is the angle of the prism.
Step 7: Calculate the Refractive Index
Since the angle A is 60 degrees:
μ=1sin(60∘)=1√32=2√3
Final Answer
The refractive index of the material of the prism is:
μ=2√3
---
We have a regular glass prism ABC with a ray LM of monochromatic light incident normally on surface AB. The angle of the prism (angle A) is given as 60 degrees.
Since the ray LM is incident normally on surface AB, it will not bend at this surface. When it reaches the surface AC, it forms an angle of 60 degrees with the normal. Therefore, the angle MNP (the angle of refraction at surface AC) is also 60 degrees.
At the surface AC, we can apply Snell's law, which states:
n1sin(θ1)=n2sin(θ2)
Where:
- n1 is the refractive index of air (approximately 1),
- θ1 is the angle of incidence (which is 60 degrees),
- n2 is the refractive index of the prism (which we need to find),
- θ2 is the angle of refraction (which is also 60 degrees).
Substituting the known values into Snell's law:
1⋅sin(60∘)=n2⋅sin(60∘)
Since sin(60∘) is common on both sides, we can simplify:
1=n2
From the equation, we can see that:
n2=1
μ=1sin(A/2)
where A is the angle of the prism.
Since the angle A is 60 degrees:
μ=1sin(60∘)=1√32=2√3
The refractive index of the material of the prism is:
μ=2√3
Similar Questions
A ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes thorugh the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
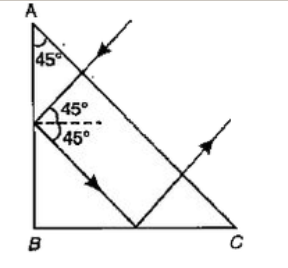
View SolutionA ray of light LM incident normally on the surface AC of an isosceles right angled prism ABC (where AB=BC) emerges along PQ, parallel to LM, as shown in given figure. What can you say about refractive index μ of the material of the prism ?
View SolutionAt what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC ?

View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionA ray of light LM incident normally on the surface AC of an isosceles right angled prism ABC (where AB = BC) emerges along PQ, parallel to LM, as shown in given figure.
What can you say about refractive index fe of the material of the prism?
View SolutionA ray EF of monochromatic light is incident on the refracting surface AB of a regular glass prism ( refractive index=1.5) at angle of incidence i=55∘ (Figure). If it emerges the adjacent face AC, calculate the angle of emergence .e..
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View SolutionA ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
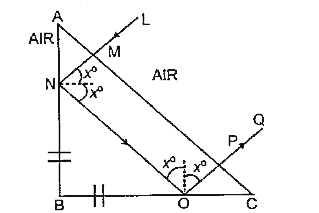
View SolutionA ray OP of monochromatic light is incident on the face AB of prism ABCD mear vertex B at an incident angle of 60degree (see figure). If the refractive index of the material of the prism is √3, which of the following is (are) are correct?

View SolutionFind the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC. (Refractive index of glass =1.6.)
View Solution