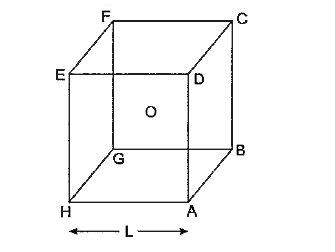
A short electric dipole (which consists of two point charges, +qand−q) is placed at the centre O and inside a large cube (ABCDEFGH) of length L, as shown in figure. The electric flux, emanating through the cube is :
q/4πε0L
zero
q/2πε0L
q/3πε0L
To solve the problem of finding the electric flux emanating through a cube that contains a short electric dipole, we can follow these steps:
1. Understand the Configuration:
- We have a short electric dipole consisting of two point charges: a positive charge +q and a negative charge −q.
- The dipole is placed at the center O of a cube with vertices labeled A,B,C,D,E,F,G,H and side length L.
2. Identify the Total Charge Enclosed:
- The total charge enclosed by the cube can be calculated by summing the charges within it.
- Since the dipole consists of one positive charge +q and one negative charge −q, the total charge enclosed is:
Qenclosed=+q+(−q)=0
3. Apply Gauss's Law:
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- Here, ϵ0 is the permittivity of free space.
4. Calculate the Electric Flux:
- Substituting the total charge enclosed into Gauss's Law:
Φ=0ϵ0=0
5. Conclusion:
- The electric flux emanating through the cube is 0.
Final Answer:
The electric flux through the cube is 0.
- We have a short electric dipole consisting of two point charges: a positive charge +q and a negative charge −q.
- The dipole is placed at the center O of a cube with vertices labeled A,B,C,D,E,F,G,H and side length L.
- The total charge enclosed by the cube can be calculated by summing the charges within it.
- Since the dipole consists of one positive charge +q and one negative charge −q, the total charge enclosed is:
Qenclosed=+q+(−q)=0
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- Here, ϵ0 is the permittivity of free space.
- Substituting the total charge enclosed into Gauss's Law:
Φ=0ϵ0=0
- The electric flux emanating through the cube is 0.
The electric flux through the cube is 0.
Similar Questions
A charge q is placed at the centre of the cubical vessel (with one face a open) as shown in figure. The flux of the electric field through the complete vessel is

View Solution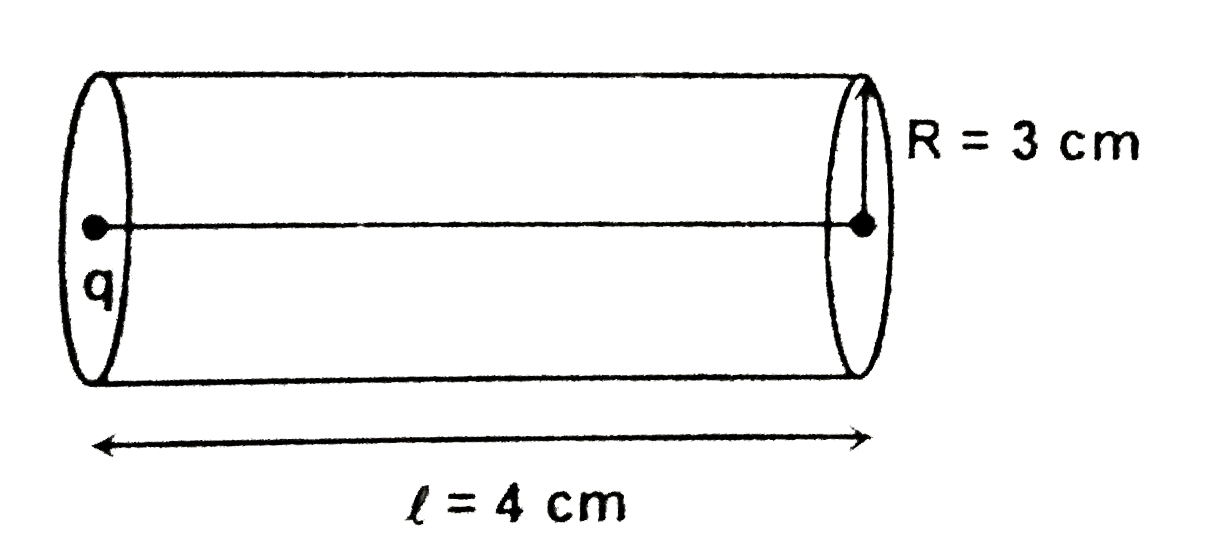
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder is
View Solution
Knowledge Check
A short electric dipole (which consists of two point charges, + q and -9) is placed at the centre o and inside a large cube (ABCDEFGH) of length L, as shown in figure below. The electric flux, emanating through the cube is :
 Aq/4πε0LBZeroCq/2πε0LDq/3πε0L
Aq/4πε0LBZeroCq/2πε0LDq/3πε0L
Two point charges 17.7 μC and -17.7μC, separated by a very small distance, are kept inside a large hollow metallic sphere. Electric flux emanating through the sphere is:
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionA point charge 'q' is placed at a distance l' (on th y-axis) vertically above the surface which lies in the xz plane as shown in the figure. The flux of electric field passing through the plate is

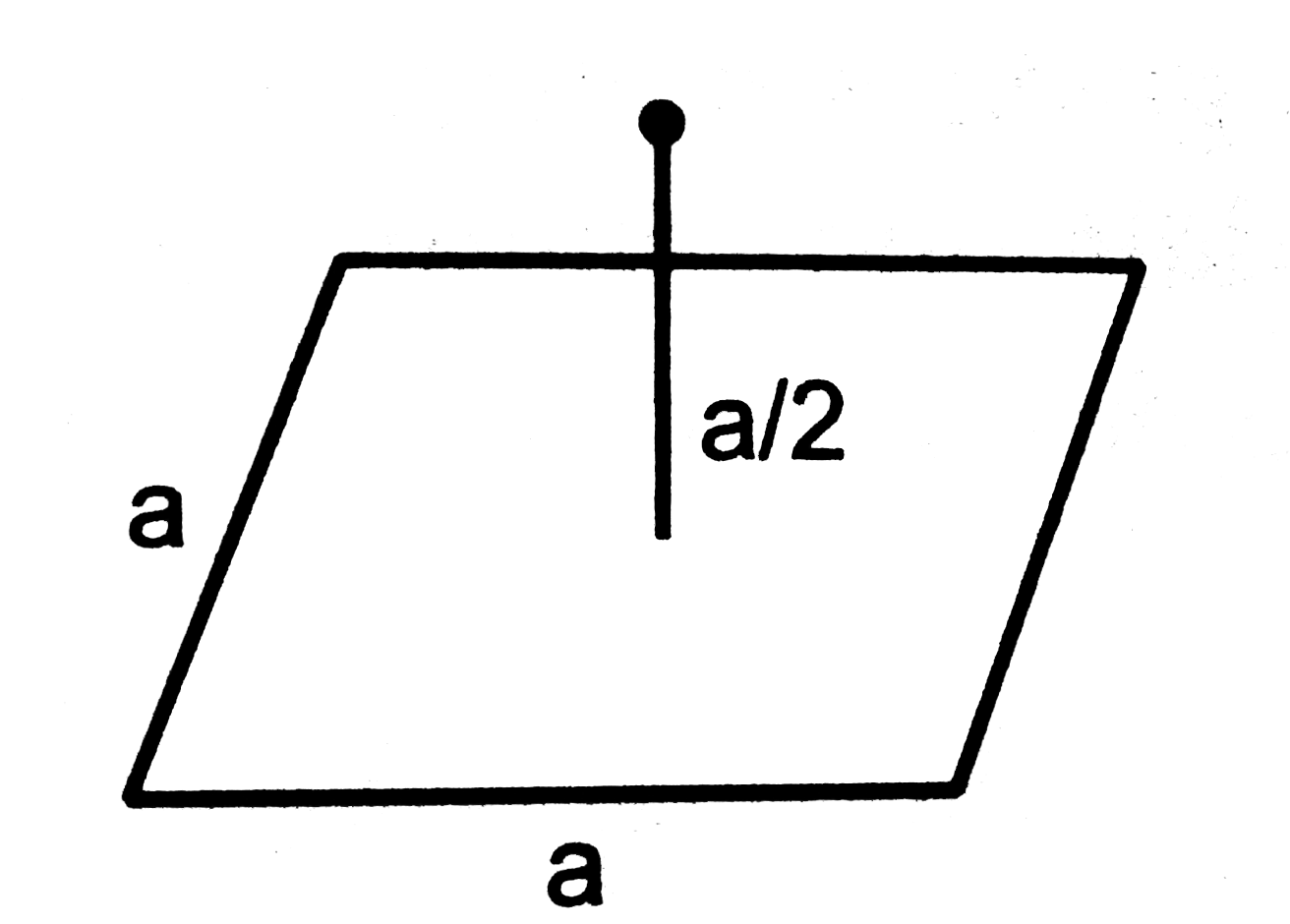
View SolutionA charge Q is placed at a distance a2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
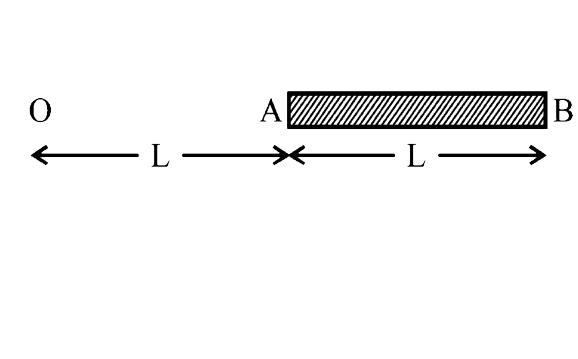
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
View SolutionIn figure +Q charge is located at one of the edge of the cube as shown in figure-1.376. Then electric flux through cube due to +Q charge is given as

View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is

View Solution
