With the help of a neatly drawn labelled diagram, prove that the magnitude of motional emf .e. is given by e=Blv, where .I. is the length of a metallic rod and v is the velocity with which it is pulled in a transverse magnetic field .B..
To prove that the magnitude of motional EMF e is given by the equation e=Blv, where l is the length of a metallic rod and v is the velocity with which it is pulled in a transverse magnetic field B, we can follow these steps:
Step 1: Set up the scenario
Consider a metallic rod of length l that is moving with a velocity v in a magnetic field B. The magnetic field is directed perpendicular to the direction of motion of the rod.
Hint: Visualize the rod moving in a magnetic field and identify the directions of the velocity and magnetic field.
Step 2: Identify the forces acting on the free electrons
As the rod moves through the magnetic field, free electrons in the rod experience a magnetic force due to the Lorentz force law. The force acting on a charge q moving with velocity v in a magnetic field B is given by:
→F=q(→v×→B)
Hint: Remember that the direction of the magnetic force can be determined using the right-hand rule.
Step 3: Determine the direction of charge separation
The magnetic force will cause the free electrons to accumulate at one end of the rod, leading to a negative charge at that end and a positive charge at the opposite end. This charge separation creates an electric field E within the rod.
Hint: Consider the implications of the charge separation on the potential difference across the rod.
Step 4: Equate magnetic force and electric force
At equilibrium, the electric force acting on the electrons due to the electric field E will balance the magnetic force. The electric force Fe can be expressed as:
Fe=qE
The magnetic force Fm can be expressed as:
Fm=qvB
Setting these two forces equal gives:
qE=qvB
Cancelling q (assuming q≠0) results in:
E=vB
Hint: Ensure you understand how the forces balance each other out.
Step 5: Relate electric field to motional EMF
The electric field E is related to the potential difference V across the length l of the rod by:
E=Vl
Substituting this into the previous equation gives:
Vl=vB
Hint: Think about how electric field relates to potential difference and length.
Step 6: Solve for the motional EMF
Rearranging the equation yields:
V=Blv
Thus, the motional EMF e is given by:
e=Blv
Hint: This final equation shows the relationship between the motional EMF, magnetic field, length of the rod, and its velocity.
Conclusion
We have proven that the magnitude of motional EMF e is given by the equation e=Blv for a metallic rod moving in a transverse magnetic field.
Consider a metallic rod of length l that is moving with a velocity v in a magnetic field B. The magnetic field is directed perpendicular to the direction of motion of the rod.
As the rod moves through the magnetic field, free electrons in the rod experience a magnetic force due to the Lorentz force law. The force acting on a charge q moving with velocity v in a magnetic field B is given by:
→F=q(→v×→B)
The magnetic force will cause the free electrons to accumulate at one end of the rod, leading to a negative charge at that end and a positive charge at the opposite end. This charge separation creates an electric field E within the rod.
At equilibrium, the electric force acting on the electrons due to the electric field E will balance the magnetic force. The electric force Fe can be expressed as:
Fe=qE
The magnetic force Fm can be expressed as:
Fm=qvB
Setting these two forces equal gives:
qE=qvB
Cancelling q (assuming q≠0) results in:
E=vB
The electric field E is related to the potential difference V across the length l of the rod by:
E=Vl
Substituting this into the previous equation gives:
Vl=vB
Rearranging the equation yields:
V=Blv
Thus, the motional EMF e is given by:
e=Blv
We have proven that the magnitude of motional EMF e is given by the equation e=Blv for a metallic rod moving in a transverse magnetic field.
Similar Questions
An electron is moving on a circular path of radius r with speed v in a transverse magnetic field B. e/m for it will be
View SolutionCurrent i is carried in a wire of length L. If the wire is turned into a circular coil, the maximum magnitude of torque in a given magnetic field B will be
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionIn Thomson.s experiment, prove that the ratio of charge to the mass (e/m) of an electron is given by :
em=12V.E2B2
where the terms have their usual meaning.
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
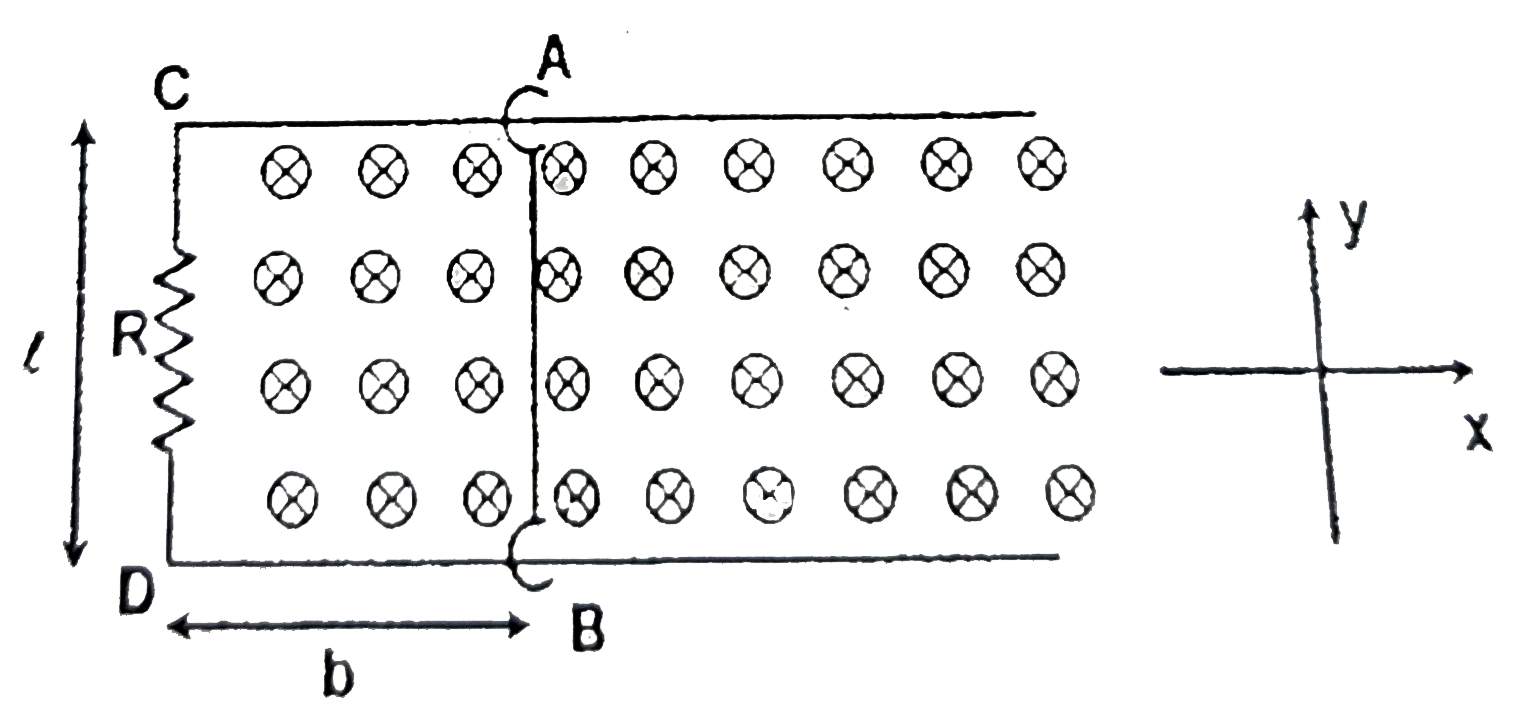
View SolutionA conducting movable rod AB lies across the frictionless parallel conducting rails in a uniform magnetic field →B whose magnitude at t=0 is B0. The rod AB is given velocity v right ward and it continues to move with same velocity through out the motion [The acceleration due to gravity is along negative z−axis, i.e. →g=10m/s2(−ˆk), mass of rod =m.] Which of the following graphs will be the best representation of magnitude of magnetic field versus time.
View SolutionA metallic V shaped rod OAC is rotated with respect to one of its end in uniform magnetic field, such that axis of rotation is parallel to the direction of magnetic field. Length of each arm of rod is L and angle between the arms is 60∘. P is the mid-point of section AC. Magnitude of magnetic field is B. Then choose the correct relation:
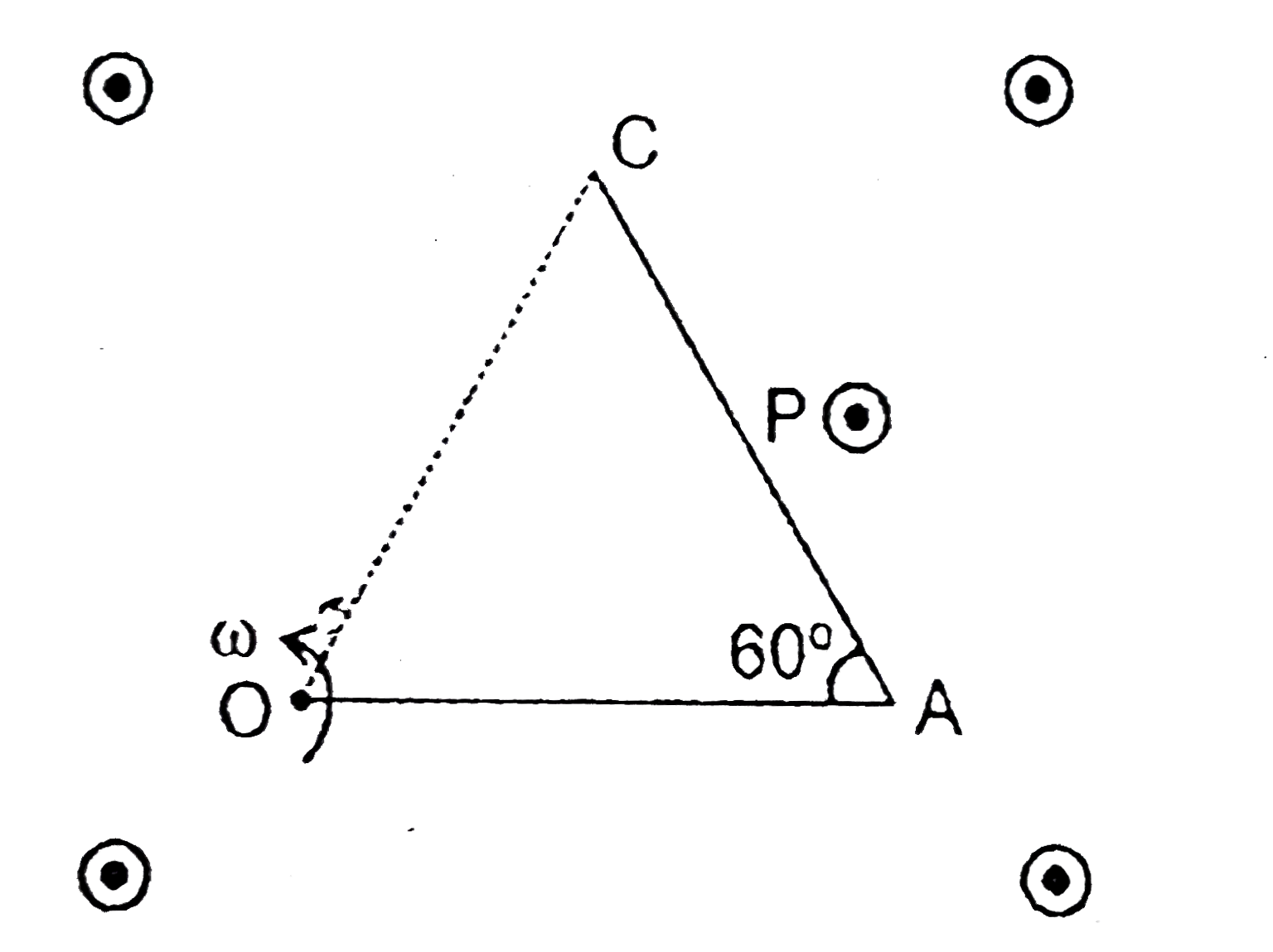
View SolutionA metallic V shaped rod OAC is rotated with respect to one of its end in uniform magnetic field, such that axis of rotation is parallel to the direction of magnetic field. Length of each arm of rod is L and angle between the arms is 60∘. P is the mid-point of section AC. Magnitude of magnetic field is B. Then choose the correct relation:

View SolutionA conducting rod of length l slides at constant velocity v on two parallel conducting rails, placed in a uniform and constant magnetic field B perpendicular to the plane of the rails as shown in Fig.3.49. A resistance R is connected between the two ends of the rails.

(a) Idenify the cause which produces change in magnetic flux.
(b) Identify the direction of current in the loop.
( c) Determine the emf induced in the loop.
(d) Compute the electric power dissipated in the resistor.
(e) Calcualte the mechenical power required to pull the rod at a cinstant velovity.
View Solution
