A ray of light incident normally on one face of a right isosceles prism is totally reflected. What must be the minimum value of refractive index of glass ? Give relevant calculations.
To solve the problem, we need to determine the minimum value of the refractive index of a right isosceles prism when a ray of light is incident normally on one face and is totally reflected at the other face.
1. Understanding the Prism:
- A right isosceles prism has two equal angles of 45 degrees and a right angle (90 degrees) between them.
- Let’s denote the refractive index of the prism as μ.
2. Incident Ray:
- The ray of light is incident normally on one face of the prism. This means that the angle of incidence i is 0 degrees.
- According to Snell's law, when light passes from air (with a refractive index of approximately 1) into the prism, the angle of refraction r will also be 0 degrees.
3. Refraction at the First Face:
- Since the ray is incident normally, it will pass straight through the prism without bending. Thus, it continues at 0 degrees into the prism.
4. Total Internal Reflection:
- The ray will reach the second face of the prism, where it will encounter the boundary between the glass and air.
- For total internal reflection to occur, the angle of incidence at this face must be greater than the critical angle.
5. Finding the Critical Angle:
- The critical angle C can be calculated using the formula:
sinC=n2n1
- Here, n1 is the refractive index of the prism (glass) and n2 is the refractive index of air (approximately 1).
6. Calculating the Critical Angle:
- For a right isosceles prism, the angle of incidence at the second face when the ray exits is 45 degrees (since the internal angles of the prism are 45 degrees).
- Therefore, we set the critical angle C to 45 degrees:
sin45∘=1√2
- Substituting into the critical angle formula gives:
1√2=1μ
7. Solving for the Refractive Index:
- Rearranging the equation gives:
μ=√2
- Numerically, this is approximately:
μ≈1.414
8. Conclusion:
- The minimum value of the refractive index of the glass required for total internal reflection in a right isosceles prism is μ=1.414.
- A right isosceles prism has two equal angles of 45 degrees and a right angle (90 degrees) between them.
- Let’s denote the refractive index of the prism as μ.
- The ray of light is incident normally on one face of the prism. This means that the angle of incidence i is 0 degrees.
- According to Snell's law, when light passes from air (with a refractive index of approximately 1) into the prism, the angle of refraction r will also be 0 degrees.
- Since the ray is incident normally, it will pass straight through the prism without bending. Thus, it continues at 0 degrees into the prism.
- The ray will reach the second face of the prism, where it will encounter the boundary between the glass and air.
- For total internal reflection to occur, the angle of incidence at this face must be greater than the critical angle.
- The critical angle C can be calculated using the formula:
sinC=n2n1
- Here, n1 is the refractive index of the prism (glass) and n2 is the refractive index of air (approximately 1).
- For a right isosceles prism, the angle of incidence at the second face when the ray exits is 45 degrees (since the internal angles of the prism are 45 degrees).
- Therefore, we set the critical angle C to 45 degrees:
sin45∘=1√2
- Substituting into the critical angle formula gives:
1√2=1μ
- Rearranging the equation gives:
μ=√2
- Numerically, this is approximately:
μ≈1.414
- The minimum value of the refractive index of the glass required for total internal reflection in a right isosceles prism is μ=1.414.
Similar Questions
(i) Plot a graph to show variation of the angle of deviation as function of angle of incidence for light passing through a prism. Derive an expression for refractive index of the prism in terms of angle of minimum deviation and angles of prism.
(ii) What is dispersion of light ? Why is its cause ?
(iii) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in fig . what must be the minimum value of refractive index of glass ? Give relevant calculations

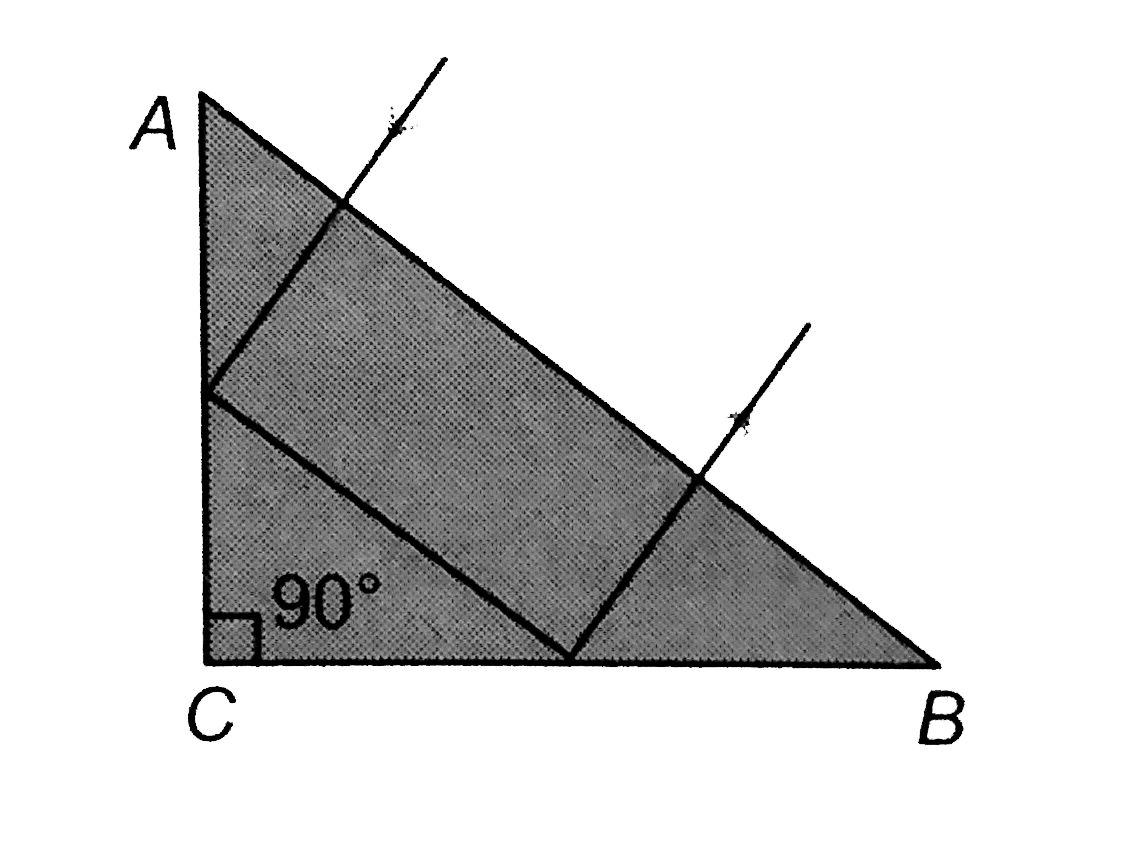
View SolutionA ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
View SolutionA ray of light is incident normally on one face of 30∘−60∘−90∘ prism of refractive index 5/3 immersed in water of refractive index 4/3 as shown in figure .
_E01_076_Q01.png)
View SolutionA trianglular prims of glass is shown in the figure. A ray incident normally to one face is totally reflected. If θ=45∘ the refractive index of glass is

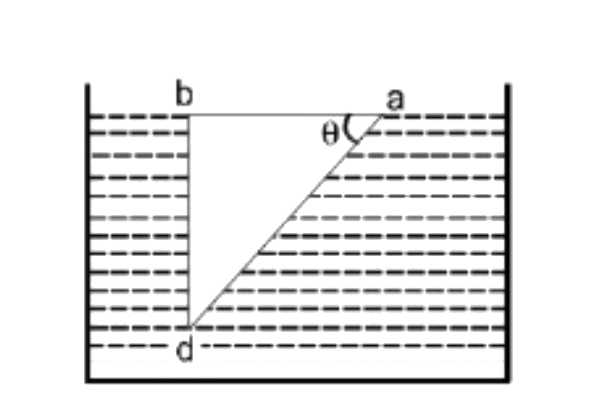
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
View SolutionA ray of light is incident normally on one face of an equilateral prism of refractive index 1.5. The angle of deviation is: (Given sin−1.23=42∘)
View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index √2. The angle of deviation of the ray in degrees is
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View Solution
