Question

When an alternating emf e = 310 sin $\left(100\pi t\right)$ V is applied to a series LCR circuit, current flowing through the circuit can be given by $i=5\sin (100\pi t+\pi /3)A$.
(1) What is the phase difference between the current and the emf ?
(2) Calculate the average power consumed by the circuit.

Explanation

To solve the problem step by step, we will address both parts of the question regarding the phase difference and the average power consumed in the circuit.

Step 1: Identify the given equations
The alternating emf and current are given as:
- \( e = 310 \sin(100\pi t) \) V
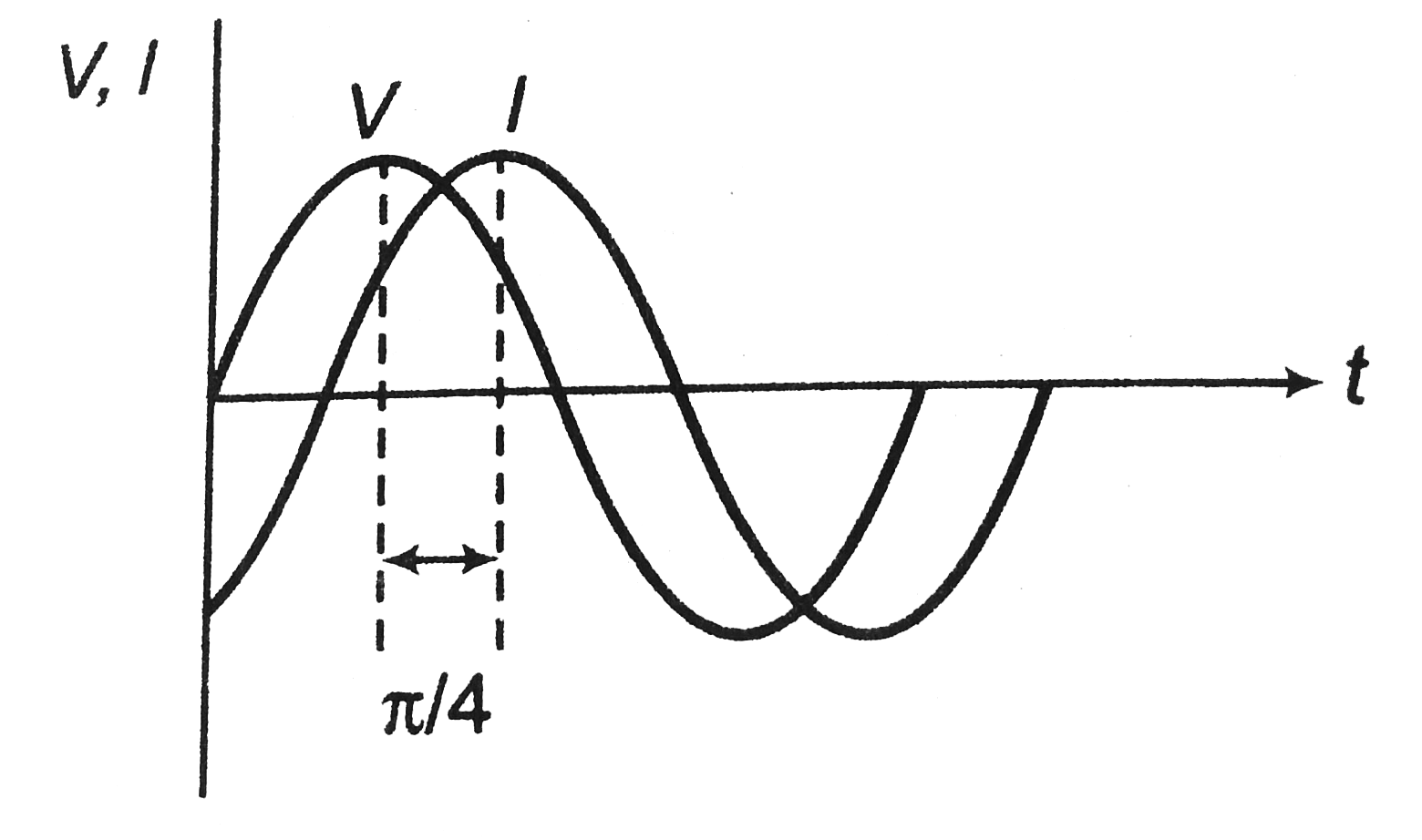
- \( i = 5 \sin(100\pi t + \frac{\pi}{3}) \) A

Step 2: Determine the phase difference
The phase of the emf is \( 0 \) (since it can be written as \( 310 \sin(100\pi t + 0) \)), and the phase of the current is \( \frac{\pi}{3} \).

The phase difference \( \phi \) between the current and the emf can be calculated as:
\( \phi = \text{Phase of current} - \text{Phase of emf} = \frac{\pi}{3} - 0 = \frac{\pi}{3} \)

Step 3: State the result for phase difference
Thus, the phase difference between the current and the emf is:
\( \phi = \frac{\pi}{3} \)

Step 4: Calculate the average power consumed by the circuit
The formula for average power \( P_{\text{avg}} \) consumed in an LCR circuit is given by:
\( P_{\text{avg}} = \frac{1}{2} I_0 V_0 \cos \phi \)
where:
- \( I_0 \) is the maximum current,
- \( V_0 \) is the maximum voltage,
- \( \phi \) is the phase difference.

From the equations:
- \( I_0 = 5 \) A (from the current equation)
- \( V_0 = 310 \) V (from the emf equation)
- \( \phi = \frac{\pi}{3} \)

Step 5: Substitute values into the power formula
Now substituting the values into the power formula:
\( P_{\text{avg}} = \frac{1}{2} \times 5 \times 310 \times \cos\left(\frac{\pi}{3}\right) \)

Step 6: Calculate \( \cos\left(\frac{\pi}{3}\right) \)
We know that:
\( \cos\left(\frac{\pi}{3}\right) = \frac{1}{2} \)

Step 7: Substitute \( \cos\left(\frac{\pi}{3}\right) \) into the power formula
Now substituting this value back into the equation:
\( P_{\text{avg}} = \frac{1}{2} \times 5 \times 310 \times \frac{1}{2} \)
\( P_{\text{avg}} = \frac{5 \times 310}{4} \)
\( P_{\text{avg}} = \frac{1550}{4} = 387.5 \text{ W} \)

Final Result
Thus, the average power consumed by the circuit is:
\( P_{\text{avg}} = 387.5 \text{ W} \)