Obtain an expression for electric potential .V due to a point charge .Q at a distance r.
To derive the expression for electric potential V due to a point charge Q at a distance r, we will follow these steps:
Step 1: Understand the Electric Field due to a Point Charge
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is the Coulomb's constant, which can also be expressed as:
k=14πϵ0
Here, ϵ0 is the permittivity of free space.
Step 2: Definition of Electric Potential
The electric potential V at a point in an electric field is defined as the work done in bringing a unit positive charge from infinity to that point against the electric field. Mathematically, this is expressed as:
dV=−→E⋅d→l
where d→l is the displacement vector.
Step 3: Setting Up the Integral
When moving a test charge from infinity (where the potential is taken as zero) to a point P at distance r, we can express the potential difference as:
V=−∫r∞→E⋅d→l
Since the electric field and the displacement are in opposite directions, we can write:
d→l=−dr^r
Thus, the dot product becomes:
→E⋅d→l=Edr
Step 4: Substitute the Electric Field
Substituting the expression for E:
V=−∫r∞kQr2(−dr)=∫r∞kQr2dr
Step 5: Evaluate the Integral
Now, we evaluate the integral:
V=kQ∫r∞1r2dr
The integral of 1r2 is:
∫1r2dr=−1r
Thus, we have:
V=kQ(−1r)r∞=kQ(−1r+0)=−kQr
Step 6: Final Expression for Electric Potential
Since V is negative due to the convention of work done against the electric field, we can express it as:
V=kQr
Substituting k back in, we get:
V=14πϵ0⋅Qr
Final Result
Thus, the expression for electric potential V due to a point charge Q at a distance r is:
V=14πϵ0⋅Qr
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is the Coulomb's constant, which can also be expressed as:
k=14πϵ0
Here, ϵ0 is the permittivity of free space.
The electric potential V at a point in an electric field is defined as the work done in bringing a unit positive charge from infinity to that point against the electric field. Mathematically, this is expressed as:
dV=−→E⋅d→l
where d→l is the displacement vector.
When moving a test charge from infinity (where the potential is taken as zero) to a point P at distance r, we can express the potential difference as:
V=−∫r∞→E⋅d→l
Since the electric field and the displacement are in opposite directions, we can write:
d→l=−dr^r
Thus, the dot product becomes:
→E⋅d→l=Edr
Substituting the expression for E:
V=−∫r∞kQr2(−dr)=∫r∞kQr2dr
Now, we evaluate the integral:
V=kQ∫r∞1r2dr
The integral of 1r2 is:
∫1r2dr=−1r
Thus, we have:
V=kQ(−1r)r∞=kQ(−1r+0)=−kQr
Since V is negative due to the convention of work done against the electric field, we can express it as:
V=kQr
Substituting k back in, we get:
V=14πϵ0⋅Qr
Thus, the expression for electric potential V due to a point charge Q at a distance r is:
V=14πϵ0⋅Qr
Similar Questions
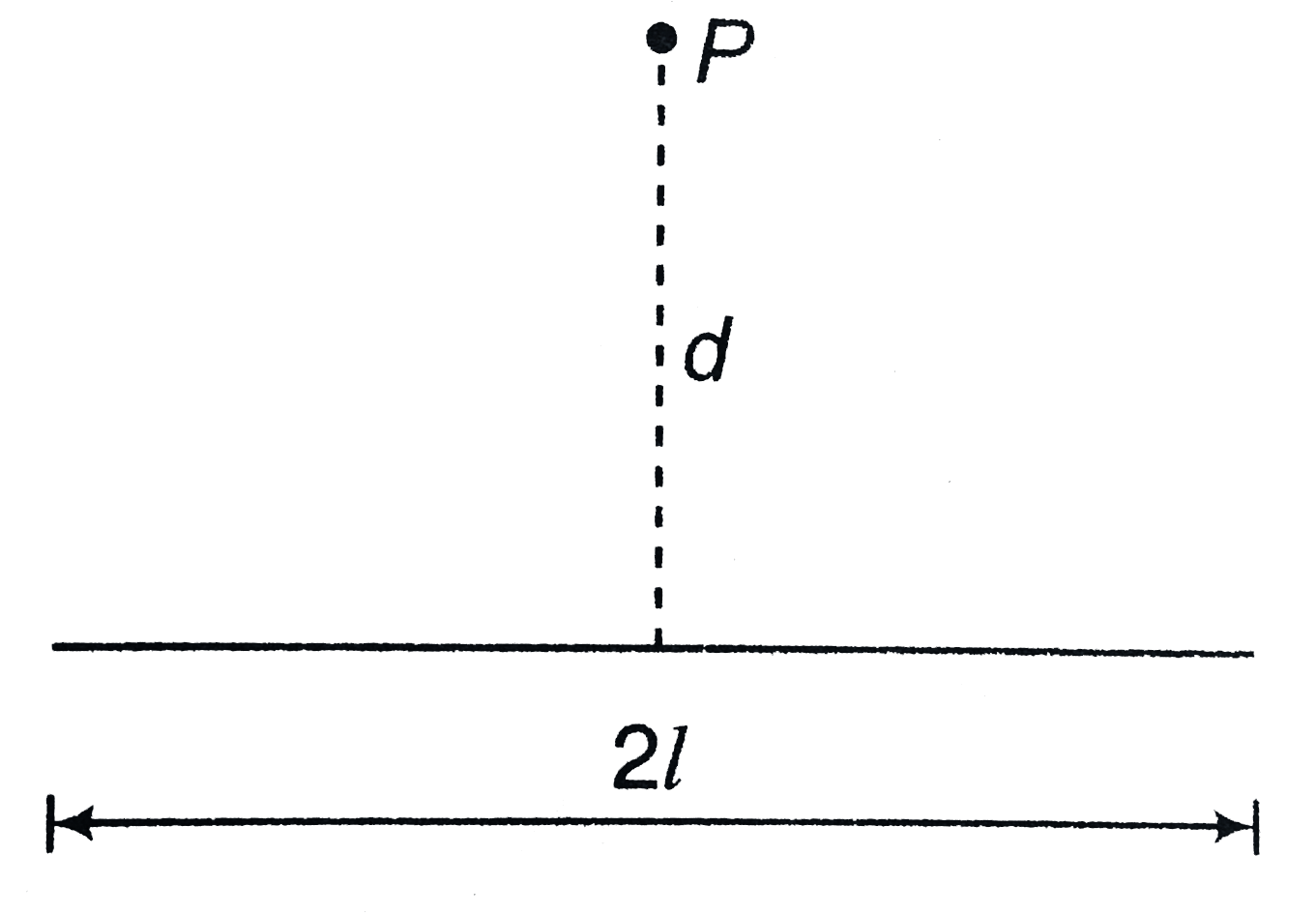
A charge q is uniformly distributed along an insulating straight wire of length 2l as shown in Fig. Find an expression for the electric potential at a point located a distance d from the distribution along its perpendicular bisector.
 View Solution
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View SolutionState the Biot-Savart law which gives the magnetic field B at a distance r from a current element. Hence obtain an expression for the magnetic field BQ due to a point charge Q moving with constant velocity v (assumed non-relativistic).
Point charge Q and Q' are constrained to move along the x-and y-axes, respectively, with the same uniform speed v. AT time t = 0 both charges are at the origin. At time t calculate the Lorentz force F on Q' due to the magnetic field of QView SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionA charge is distributed uniformly over a ring of radius 'a'. Obtain an expression for the electric intensity E at a point on the axis of the ring . Hence show that for points at large distances from the ring it behaves like a point charge .
View SolutionA charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is
View Solution
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' isView SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View Solution

