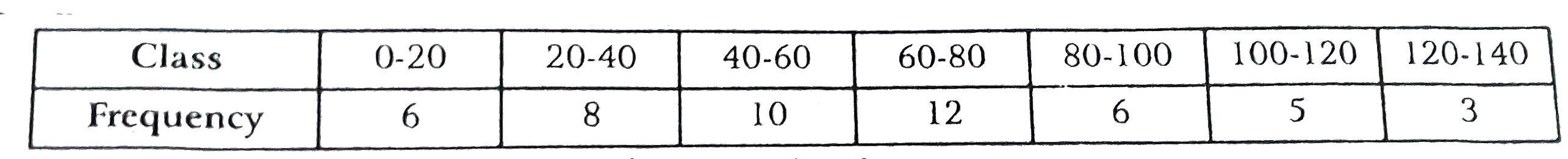If the mean and the mode of a moderately skewed frequency distribution are 90 and 96 respectively, then the median is
93
92
98
88
The correct Answer is:B
To find the median of a moderately skewed frequency distribution when the mean and mode are given, we can use the relationship between mean, median, and mode.
1. Identify the given values:
- Mean (M) = 90
- Mode (Mo) = 96
2. Use the formula relating mean, median, and mode:
The formula is:
Mo=3×Median−2×M
Rearranging this formula to find the median gives:
Median=Mo+2M3
3. Substitute the known values into the formula:
Median=96+2×903
4. Calculate the value:
- First, calculate 2×90:
2×90=180
- Now add this to the mode:
96+180=276
- Finally, divide by 3:
Median=2763=92
5. Conclusion:
The median of the frequency distribution is 92.
- Mean (M) = 90
- Mode (Mo) = 96
The formula is:
Mo=3×Median−2×M
Rearranging this formula to find the median gives:
Median=Mo+2M3
Median=96+2×903
- First, calculate 2×90:
2×90=180
- Now add this to the mode:
96+180=276
- Finally, divide by 3:
Median=2763=92
The median of the frequency distribution is 92.
Similar Questions
Knowledge Check
If the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
A68B76C75D70
The mode for the following frequency distribution :

View SolutionFind the mean for the following frequency distribution :
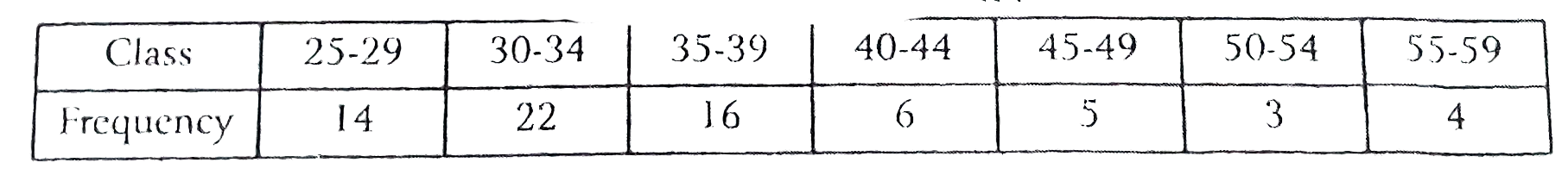
View SolutionCompute the mode for the following frequency distribution:
View SolutionCompute the mode for the following frequency distribution :

View SolutionFind the mode and median of the following frequency distribution :
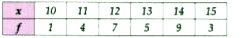
View SolutionFind the median for the following frequency distribution:
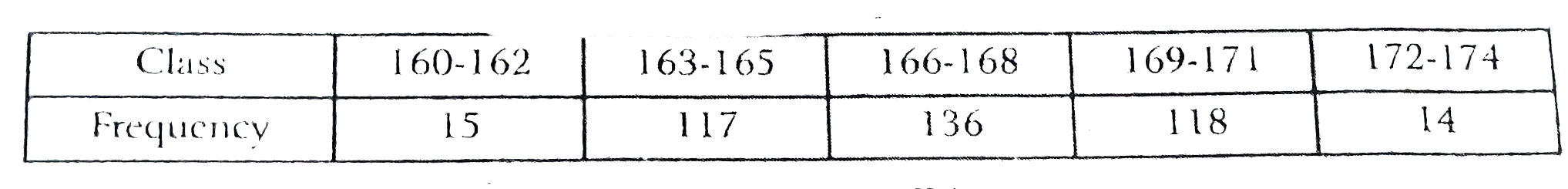
View SolutionFind the mean and variance for the following frequency distributions in
View Solution