Identify whether the given pair consists of equal or equivalent but not equal sets or none:
G= {a,b,c} and H={x,y,z}
The correct Answer is:G→H
To determine whether the sets G and H are equal, equivalent but not equal, or neither, we will follow these steps:
Step 1: Define the Sets
We have two sets:
- Set G = {a, b, c}
- Set H = {x, y, z}
Step 2: Check for Equality
Two sets are considered equal if they contain exactly the same elements.
- In this case, G contains the elements {a, b, c} and H contains the elements {x, y, z}.
- Since the elements in G are not the same as the elements in H, we conclude that G is not equal to H.
Step 3: Check for Equivalence
Two sets are considered equivalent if they have the same number of elements, regardless of what those elements are.
- Count the number of elements in each set:
- Set G has 3 elements: {a, b, c}
- Set H also has 3 elements: {x, y, z}
- Since both sets have the same number of elements (3), we conclude that G and H are equivalent.
Final Conclusion
- G and H are equivalent sets but not equal sets.
Summary
- G and H are equivalent sets.
---
We have two sets:
- Set G = {a, b, c}
- Set H = {x, y, z}
Two sets are considered equal if they contain exactly the same elements.
- In this case, G contains the elements {a, b, c} and H contains the elements {x, y, z}.
- Since the elements in G are not the same as the elements in H, we conclude that G is not equal to H.
Two sets are considered equivalent if they have the same number of elements, regardless of what those elements are.
- Count the number of elements in each set:
- Set G has 3 elements: {a, b, c}
- Set H also has 3 elements: {x, y, z}
- Since both sets have the same number of elements (3), we conclude that G and H are equivalent.
- G and H are equivalent sets but not equal sets.
- G and H are equivalent sets.
Topper's Solved these Questions
- SETS BOOK - ICSECHAPTER - SETS EXERCISE - EXERCISE 6 B
39 Videos
- SETS BOOK - ICSECHAPTER - SETS EXERCISE - EXERCISE 6 C
32 Videos
- SETS BOOK - ICSECHAPTER - SETS EXERCISE - EXERCISE 6 D
23 Videos
- REPRESENTING 3 - D IN 2- D BOOK - ICSECHAPTER - REPRESENTING 3 - D IN 2- D EXERCISE - EXERCISE 20 B
1 Videos
- SIMPLE INTERESTBOOK - ICSECHAPTER - SIMPLE INTERESTEXERCISE - Challenge
2 Videos
Similar Questions
Identify whether the given pair consists of equal or equivalent but not equal sets or none:
J= {x,x∈N,x≠x}andK={x:x∈N,6<x<7}.
View SolutionIdentify whether the given pair consists of equal or equivalent but not equal sets or none:
C = {x: x ∈N,x+5=6}andD={x:x∈W,x<1}.
View SolutionIdentify whether the given pair consists of equal or equivalent but not equal sets or none:
A = set of letters of the word 'FLOWER'
B = set of letters of the word ' FOLLOWER'
View SolutionIdentify whether the given pair consists of equal or equivalent but not equal sets or none:
E= set of first five whole numbers.
F = set of first five natural numbers.
View SolutionState, whether the following pairs of sets are equivalent or not:
A={x:x∈N and 11≥2x−1} and B={y:y∈W and 3≤y≤9}
View SolutionState, whether the following pairs of sets are equal or not:
E={x:x2+8x−9=0} and F={1,−9}
View SolutionIdentify X,Y and Z in the given sequence of reactions
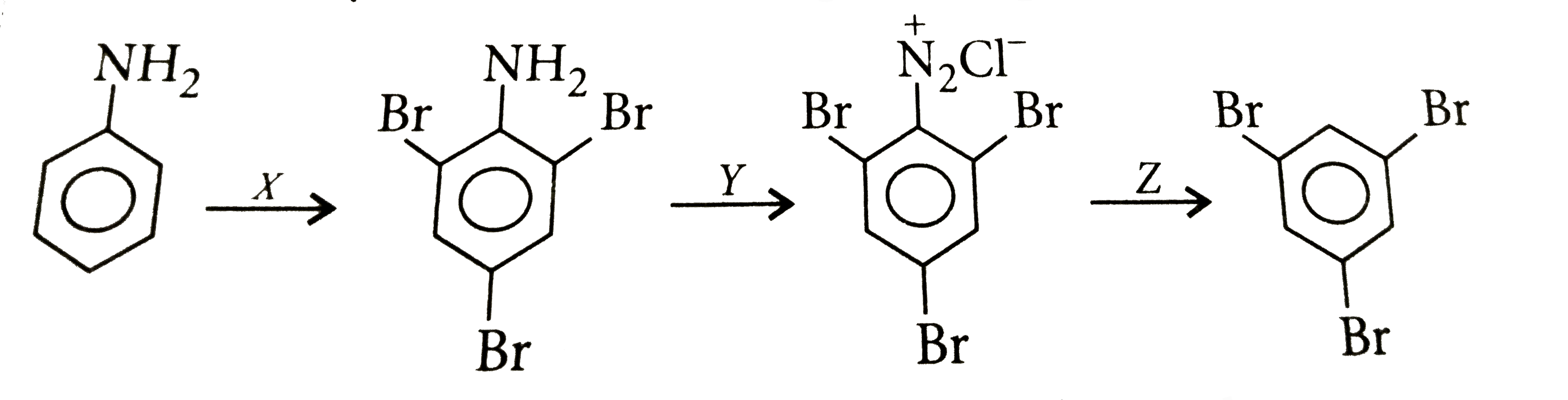
View SolutionState whether the following pairs of sets are equal or not :
A = {kids 5 metres tall}, B={x:x∈N and 2x=3}.
View SolutionState, whether the following pairs of sets are equal or not:
A={x:x∈N,x<3} and B={y:y2−3y+2=0}
View SolutionState whether the following pairs of sets are equal or not :
A = {2,4,6,8,10} , B = {even natural numbers}
View Solution
