In the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
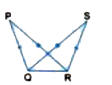
Step by step video & image solution for In the given figure, we have PQ=SR and PR=SQ. Prove that : (i) DeltaPQR~=DeltaSRQ (ii) anglePQR=angleSRQ by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given figure we have AO=BO and CO=DO. Prove that :
(i) ΔAOC≅ΔBOD
AC=BD

View SolutionIn the given figure, AB=CD and AD=CB. Prove that :
(i) ΔABD=ΔCDB
(ii) ∠A=∠C

View SolutionIn the given figure, we have AC⊥CD,BC⊥CD and DA=DB. Prove that : CA=CB.
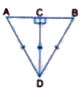
View SolutionIn the given figure, AB⊥BD,CD⊥BD and AB=CD. Prove that :
(i) ΔABD≅ΔCDB
(ii) AD-CB

View SolutionIn the given figure AB=AC and AD=AE. Prove that (i) ΔABD≅ΔACE and (ii) BE=DC
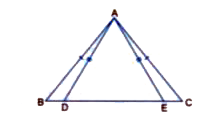
View SolutionIn the given figure, ∠SPR=∠QRP and ∠RSP=∠PQR. Prove that :
(i) PQ=RS
(ii) PS=QR

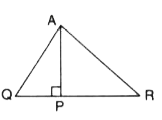
View SolutionIn the given figure, PL⊥OA and PM⊥OB such that OL=OM. Prove that :
(i) ΔOLP≅ΔOMP
(ii) PL=PM
∠LOP=∠MOP

View SolutionIn the given figure , PR>PQ
Prove that : AR>AQ
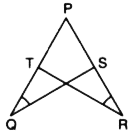
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
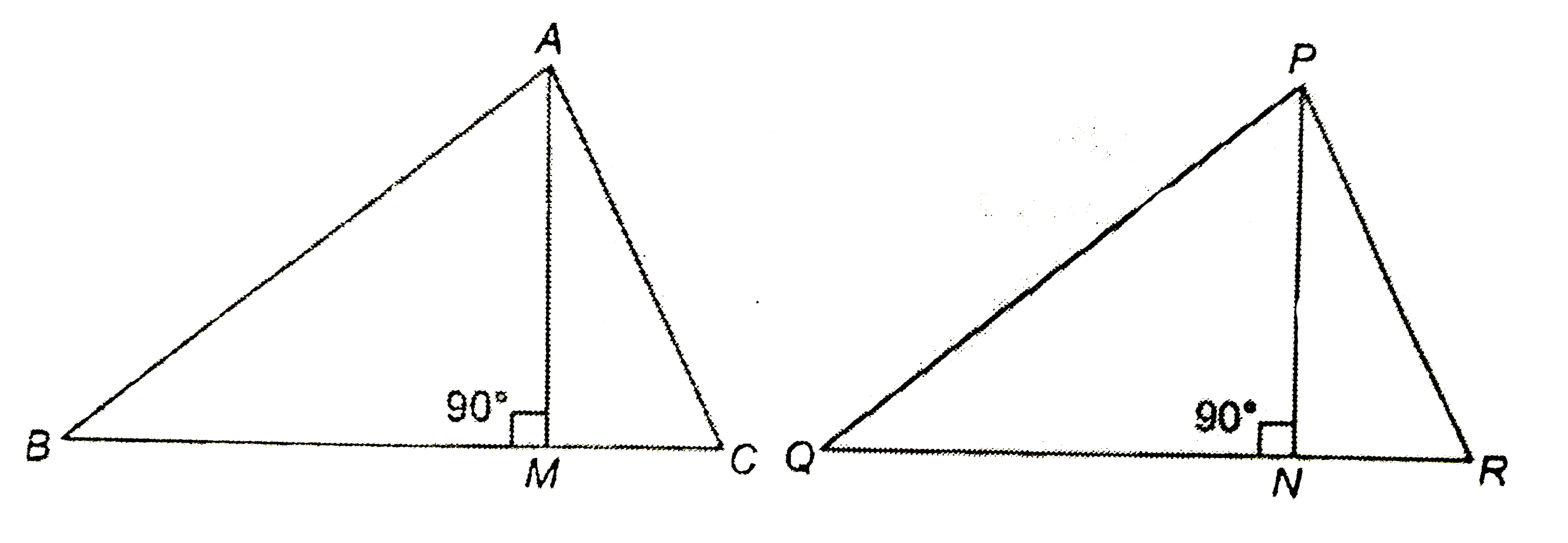
View SolutionIn the following figures, AB=PQ,AC=PR and AM=PN. Prove that ΔABC≅ΔPQR.
View Solution
