A conventional method of representing Daniell cell is:
Zn(s),Zn2+(aq)(1M)||Cu2+(aq)(1M),Cu(s)
(i) Draw a diagram of the cell and mark anode and cathode.
Cu2+/Cu=0.34V,Zn2+/Zn=−0.76V
(ii) Give the net reaction as current is drawn.
(iii) What is the cell potential at 298 K?
The correct Answer is:(ii) Zn+Cu2+→Zn2++Cu (ii) 1.10 V
Step-by-Step Solution:
1. Draw two containers: Start by sketching two beakers or containers. Label the left container as "Zinc half-cell" and the right container as "Copper half-cell".
2. Add solutions: In the left container, indicate that it contains a solution of Zinc sulfate (ZnSO₄) and in the right container, indicate that it contains Copper sulfate (CuSO₄).
3. Insert electrodes: Draw a zinc electrode (Zn) in the left container and a copper electrode (Cu) in the right container.
4. Connect with a salt bridge: Draw a salt bridge connecting the two containers. This bridge allows ions to flow between the two half-cells.
5. Mark the anode and cathode:
- Label the zinc electrode as the anode (where oxidation occurs).
- Label the copper electrode as the cathode (where reduction occurs).
6. Indicate electron flow: Draw arrows to show that electrons flow from the anode (Zn) to the cathode (Cu).
7. Label the terminals: Mark the left side (anode) as negative (-) and the right side (cathode) as positive (+).
Diagram:
Zn(s)∣∣Zn²⁺(aq)(1M)∣∣∣∣Cu²⁺(aq)(1M)∣∣Cu(s)(Anode)(Cathode)
(ii) Give the net reaction as current is drawn.
1. Write the oxidation half-reaction at the anode:
\(
\text{Zn(s)} \rightarrow \text{Zn}^{2+}(aq) + 2e^{-}
\)
2. Write the reduction half-reaction at the cathode:
\(
\text{Cu}^{2+}(aq) + 2e^{-} \rightarrow \text{Cu(s)}
\)
3. Combine the two half-reactions to get the net reaction:
- The electrons cancel out:
\(
\text{Zn(s)} + \text{Cu}^{2+}(aq) \rightarrow \text{Zn}^{2+}(aq) + \text{Cu(s)}
\)
(iii) What is the cell potential at 298 K?
1. Identify the standard reduction potentials:
- For Cu²⁺/Cu: \( E^\circ = +0.34 \, V \)
- For Zn²⁺/Zn: \( E^\circ = -0.76 \, V \)
2. Calculate the standard cell potential \( E^\circ_{cell} \):
\(
E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}
\)
\(
E^\circ_{cell} = 0.34 \, V - (-0.76 \, V) = 0.34 \, V + 0.76 \, V = 1.10 \, V
\)
3. Use the Nernst equation to find the cell potential at 298 K:
\(
E_{cell} = E^\circ_{cell} - \frac{0.0591}{n} \log \left( \frac{(\text{products})}{(\text{reactants})} \right)
\)
- Here, \( n = 2 \) (number of electrons transferred).
- Since both concentrations are 1 M, the log term becomes:
\(
\log \left( \frac{1}{1} \right) = 0
\)
4. Substituting values:
\(
E_{cell} = 1.10 \, V - \frac{0.0591}{2} \cdot 0 = 1.10 \, V
\)
Final Answers:
- (i) Diagram of the Daniell cell with anode and cathode labeled.
- (ii) Net reaction:
\(
\text{Zn(s)} + \text{Cu}^{2+}(aq) \rightarrow \text{Zn}^{2+}(aq) + \text{Cu(s)}
\)
- (iii) Cell potential at 298 K: \( E_{cell} = 1.10 \, V \)
- Label the zinc electrode as the anode (where oxidation occurs).
- Label the copper electrode as the cathode (where reduction occurs).
Zn(s)∣∣Zn²⁺(aq)(1M)∣∣∣∣Cu²⁺(aq)(1M)∣∣Cu(s)(Anode)(Cathode)
\(
\text{Zn(s)} \rightarrow \text{Zn}^{2+}(aq) + 2e^{-}
\)
\(
\text{Cu}^{2+}(aq) + 2e^{-} \rightarrow \text{Cu(s)}
\)
- The electrons cancel out:
\(
\text{Zn(s)} + \text{Cu}^{2+}(aq) \rightarrow \text{Zn}^{2+}(aq) + \text{Cu(s)}
\)
- For Cu²⁺/Cu: \( E^\circ = +0.34 \, V \)
- For Zn²⁺/Zn: \( E^\circ = -0.76 \, V \)
\(
E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}
\)
\(
E^\circ_{cell} = 0.34 \, V - (-0.76 \, V) = 0.34 \, V + 0.76 \, V = 1.10 \, V
\)
\(
E_{cell} = E^\circ_{cell} - \frac{0.0591}{n} \log \left( \frac{(\text{products})}{(\text{reactants})} \right)
\)
- Here, \( n = 2 \) (number of electrons transferred).
- Since both concentrations are 1 M, the log term becomes:
\(
\log \left( \frac{1}{1} \right) = 0
\)
\(
E_{cell} = 1.10 \, V - \frac{0.0591}{2} \cdot 0 = 1.10 \, V
\)
- (i) Diagram of the Daniell cell with anode and cathode labeled.
- (ii) Net reaction:
\(
\text{Zn(s)} + \text{Cu}^{2+}(aq) \rightarrow \text{Zn}^{2+}(aq) + \text{Cu(s)}
\)
- (iii) Cell potential at 298 K: \( E_{cell} = 1.10 \, V \)
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - ICSECHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE (PART-I Objective Questions)
28 Videos
- ELECTROCHEMISTRYBOOK - ICSECHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE (PART-I Objective Questions) (Choose the correct alternative)
25 Videos
- ELECTROCHEMISTRYBOOK - ICSECHAPTER - ELECTROCHEMISTRYEXERCISE - ISC EXAMINATION QUESTIONS (PART-II Numerical Problems)
19 Videos
- DISTINCTION BETWEEN PAIRS OF COMPOUNDS BOOK - ICSECHAPTER - DISTINCTION BETWEEN PAIRS OF COMPOUNDS EXERCISE - QUESTIONS
155 Videos
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS BOOK - ICSECHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS EXERCISE - EXERCISE (PART-I ( OBJECTIVE QUESTIONS )) (Fill in the blanks)
60 Videos
Similar Questions
Write Nernst equation for the following cell reaction :
Zn|Zn2+(aq)||Cu2+(aq)|Cu(s)
View SolutionE.M.F. of Ni(s)∣∣Ni2+(aq)∣∣∣∣Cu2+(aq)∣∣Cu(s) cell can be increased by
View SolutionE∘ for the cell
Zn(s)∣∣Zn2+(aq)∣∣Cu2+(aq)∣Cu(s) is 1.1V at 25∘C the equilibrium constant for the cell reaction is about
View SolutionThe standard cell potential of:
Zn(s)∣∣Zn2+(aq)∣∣∣∣Cu2+(aq)∣∣Cu(s) cell is 1.10 V The maximum work obtained by this cell will be
View SolutionFor the given cell arrangement identify incorrect statement
given E∘_(Cu2+/Cu) = 0.34V &E∘_(Zn2+/Zn)=−0.76V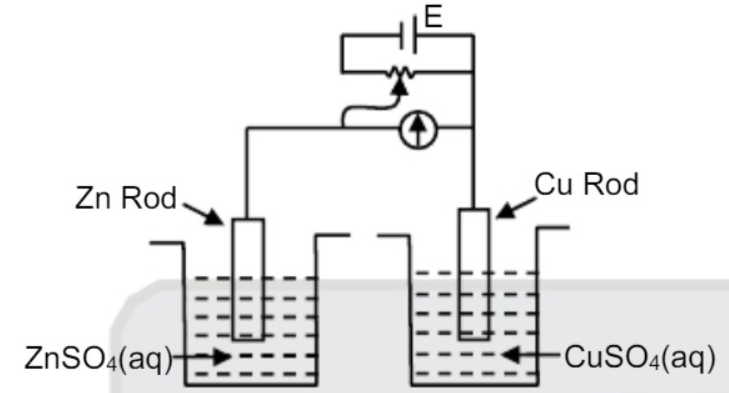
View SolutionWrite the cell reaction for each of the following cells.
Ni(s)∣∣Ni2+(aq)∣∣∣∣Cu2+(aq)∣∣Cu(s).
View SolutionE∘ for the electrochemical cell
Zn(s)∣∣Zn2+1M(Aq.)∣∣∣∣Cu2+1M(aq.)∣∣Cu(s)
is 1.10 V at 25∘C. The equilibrium constant for the cell reaction,
Zn(s)+Cu2+(aq.)⇔Zn2+(aq.)+Cu(s)
Will be :
View SolutionA Daniell cell :
Zn∣∣Zn2+∣∣∣∣Cu2+∣∣Cu with Ecell=1.1V is given. Is this a spontaneous cell?
View SolutionThe following electrochemical cell is set up at 298 K:
Zn/Zn2+(aq)(1M)∣∣Cu2+(aq)(1M)/Cu
Given: E∘Zn2+/Zn=−0.761V,E∘Cu2+/Cu=+0.339V
(1) Write the cell reaction.
(2) Calculate the emf and free energy change at 298 K
View SolutionConsider the cell :
Zn∣∣Zn2+(aq)(1.0M)∣∣∣∣Cu2+(aq)(1.0M)∣∣∣Cu
Thee standard reduction potentials are 0.350V for
Cu2+(aq)+2e−→Cu and −0.763V for
Zn2+(aq)+2e−→Zn
a. Write the cell reaction.
b. Calculate the EMF of the cell.
c. Is the reaction spontaneous or not ?
View Solution
