To get an echo, the reflecting wall should be about 17 m from the source
To solve the question regarding the distance required to hear an echo, we can follow these steps:
1. Understanding Echo: An echo is the reflection of sound that arrives at the listener after a delay. To hear an echo distinctly, there must be a sufficient time gap between the original sound and its reflection.
2. Time Gap Requirement: The human ear can distinguish between two sounds if the time gap between them is at least 0.1 seconds. This is crucial for hearing an echo.
3. Speed of Sound: The speed of sound in air is approximately 343 meters per second (m/s) at room temperature. This speed will help us calculate the distance required for an echo.
4. Calculating the Minimum Distance:
- The total distance for the sound to travel to the reflecting wall and back to the source is twice the distance to the wall.
- If we denote the distance to the wall as d, then the total distance is 2d.
- The time t taken for the sound to travel this distance can be calculated using the formula:
t=DistanceSpeed=2d343
5. Setting Up the Equation: For the echo to be heard, this time t must be greater than or equal to 0.1 seconds:
2d343≥0.1
6. Solving for d:
- Rearranging the equation gives:
2d≥0.1×343
- Calculating 0.1×343:
0.1×343=34.3
- Thus, we have:
2d≥34.3
- Dividing both sides by 2 gives:
d≥34.32=17.15 meters
7. Conclusion: Therefore, to hear an echo, the reflecting wall should be at least approximately 17 meters away from the sound source.
- The total distance for the sound to travel to the reflecting wall and back to the source is twice the distance to the wall.
- If we denote the distance to the wall as d, then the total distance is 2d.
- The time t taken for the sound to travel this distance can be calculated using the formula:
t=DistanceSpeed=2d343
2d343≥0.1
- Rearranging the equation gives:
2d≥0.1×343
- Calculating 0.1×343:
0.1×343=34.3
- Thus, we have:
2d≥34.3
- Dividing both sides by 2 gives:
d≥34.32=17.15 meters
Topper's Solved these Questions
- SOUNDBook:ICSEChapter:SOUNDExercise:EXERCISES (Section II) (Distinguish between)
Explore 5 Videos
- SOUNDBook:ICSEChapter:SOUNDExercise:EXERCISES (Section II) (Short Answer Questions)
Explore 9 Videos
- SOUNDBook:ICSEChapter:SOUNDExercise:EXERCISES (Section I) (Choose the correct option to fill in the blank)
Explore 10 Videos
- PHYSICAL QUANTITIES AND MEASUREMENTBook:ICSEChapter:PHYSICAL QUANTITIES AND MEASUREMENTExercise:EXERCISE PICTURE STUDY
Explore 3 Videos
Similar Questions
An echo is returned in 3s. What is the distance of the reflecting surface from the source, given that the speed of sound is 342m/s.
View SolutionA sound sources, detector and a movable wall are arranged as shown in figure. In this arrangement detectir us detacting the maximum intensity. If the speed of sound is 330m/s in air and frequency of source is 660Hz, then find the minimum distance by which the wall should be moved away from source, so that detector dtects minimmum intensity.

View Solution
Knowledge Check
What should be substracted from −23 to get 1?
A−83B−73C−43D−53
A stationary sound sound 's' of frequency 334 Hz and a stationary ovserver 'O' are placed near a reflecting suface moving away from the source with velocity 2 m/s as shown in the figure. If the velocity of the sound waves is air is v= 330 m/s the apparent frequency of the echo is
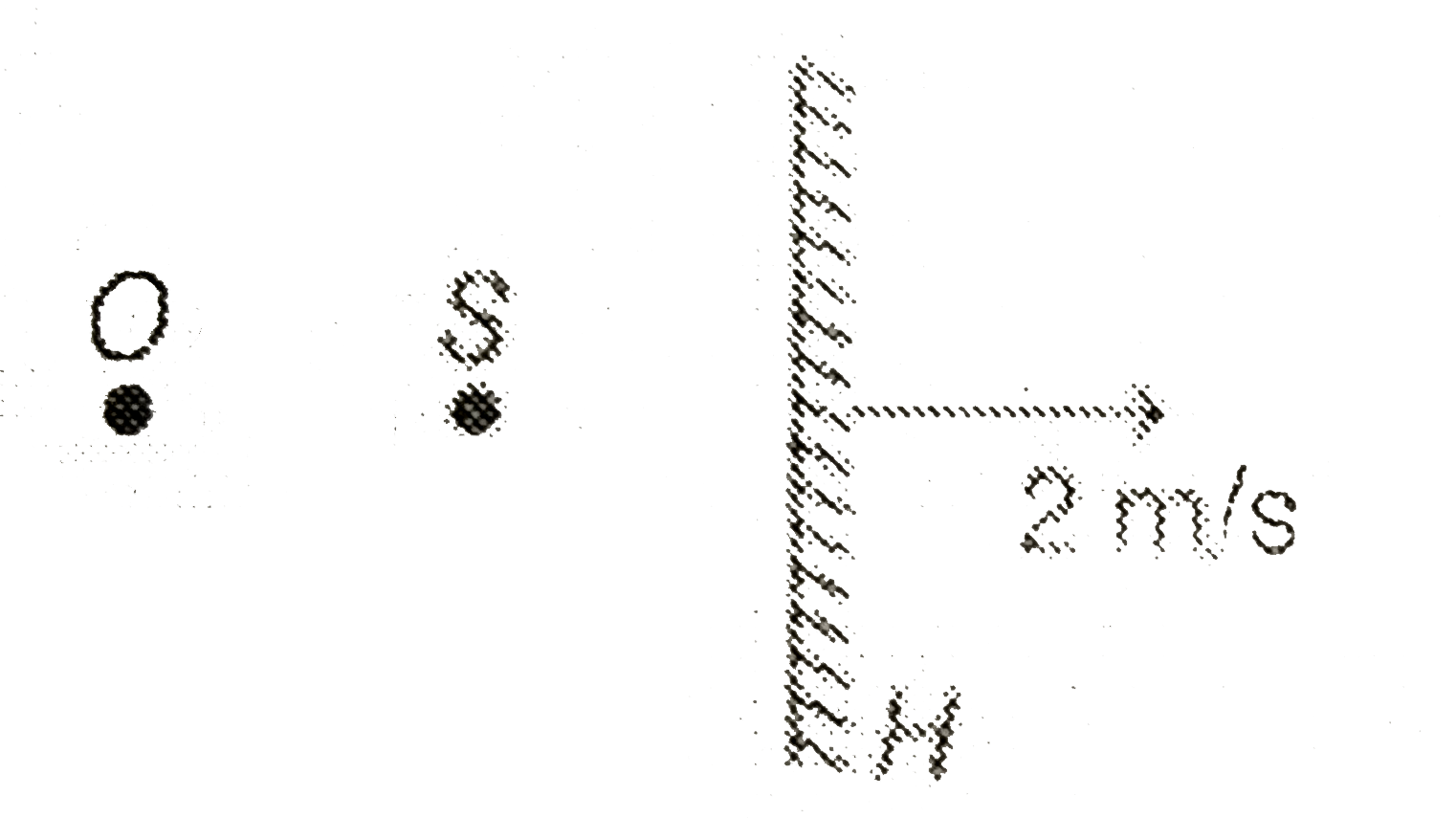
View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionSound waves of frequency 660HZ fall normally on perfectly reflecting wall. The distance from the wall at which the air particles have the maximum amplitude of vibration is (speed of sound in air = 330m/s)
View SolutionSound waves of frequency 600HZ fall normally on perfectly reflecting wall. The distance from the wall at which the air particles have the maximum amplitude of vibration is (speed of sound in air = 330m/s)
View SolutionA source of sound of frequency 300 Hz and a receiver are located along the same line normal to the wall as shown in the figure. Both the source and the receiver are stationary and the wall receeds from the source with velocity 20ms−1.If the beat frequency registered by the receiver is 240x Hz then x is :
(Assume Vsound=300 m/s).

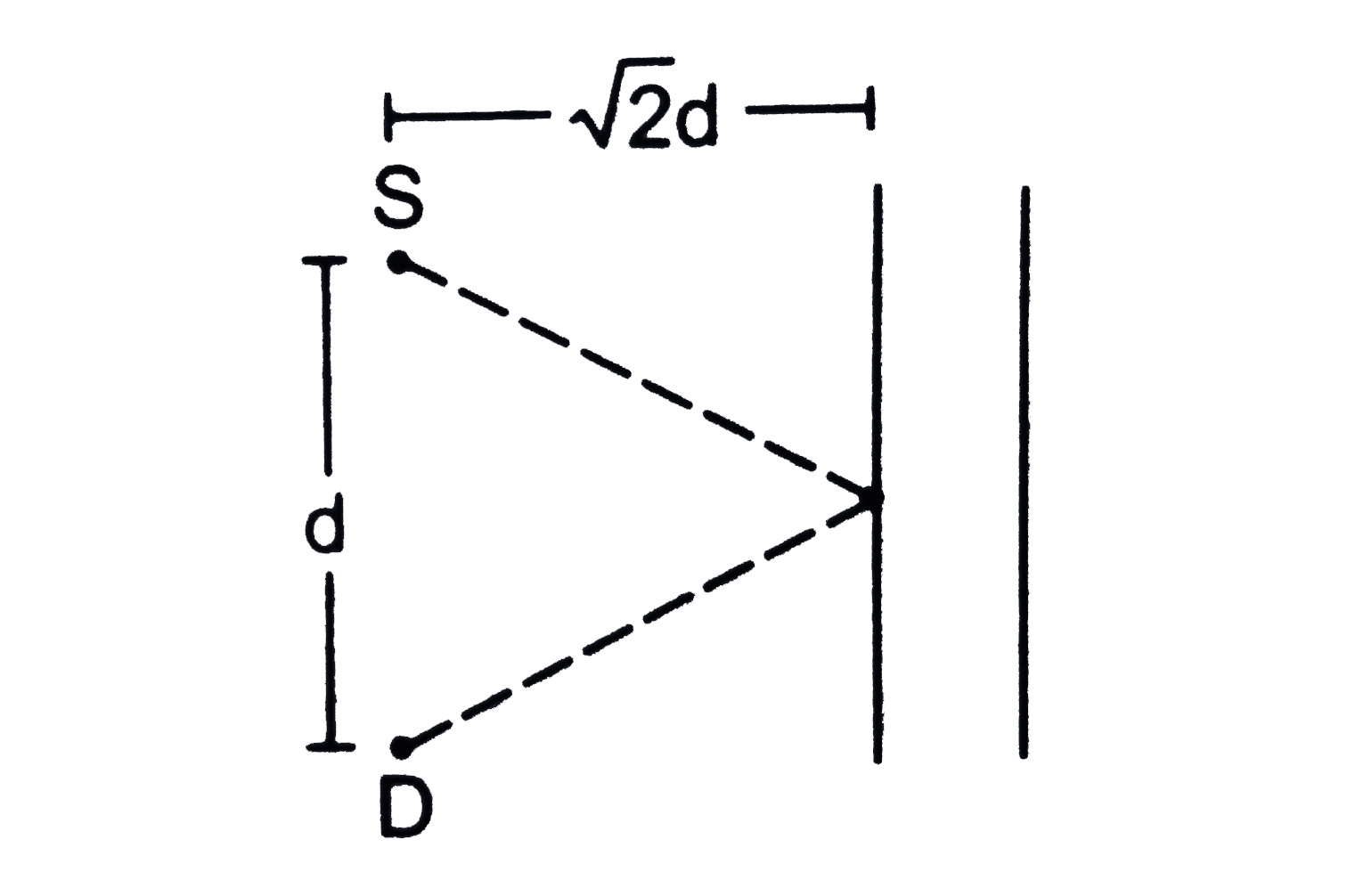
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View Solution