Which one has more energy-a car parked on the roadside or a car on the second floor of a building? Why?
To determine which car has more energy, we need to analyze the potential energy of both cars based on their positions.
1. Identify the Cars and Their Positions:
- We have two cars:
- Car 1 is parked on the roadside (ground level).
- Car 2 is parked on the second floor of a building (above ground level).
2. Understand Energy Types:
- The total energy of an object is the sum of its kinetic energy (KE) and potential energy (PE).
- Kinetic energy is related to motion, while potential energy is related to height.
3. Determine Kinetic Energy:
- Since both cars are parked, they are not moving. Therefore, the velocity of both cars is zero.
- Kinetic Energy (KE) = 0.5 * mass * velocity² = 0.5 * mass * 0² = 0.
- Thus, the kinetic energy of both cars is zero.
4. Calculate Potential Energy:
- Potential Energy (PE) is given by the formula: PE = mass * g * height, where g is the acceleration due to gravity (approximately 9.81 m/s²).
- For Car 1 (parked on the roadside):
- Height = 0 (ground level).
- PE1 = mass * g * 0 = 0.
- For Car 2 (parked on the second floor):
- Height = height of the second floor (let's assume it's a certain height, say h).
- PE2 = mass * g * h (where h > 0).
5. Compare the Potential Energies:
- Since Car 2 is at a height (h) above ground level, its potential energy (PE2) is greater than that of Car 1 (PE1 = 0).
- Therefore, PE2 > PE1.
6. Conclusion:
- Since both cars have zero kinetic energy and Car 2 has greater potential energy than Car 1, we conclude that:
- The car on the second floor (Car 2) has more total energy than the car parked on the roadside (Car 1).
Final Answer:
The car on the second floor of the building has more energy than the car parked on the roadside because it has greater potential energy due to its height.
---
- We have two cars:
- Car 1 is parked on the roadside (ground level).
- Car 2 is parked on the second floor of a building (above ground level).
- The total energy of an object is the sum of its kinetic energy (KE) and potential energy (PE).
- Kinetic energy is related to motion, while potential energy is related to height.
- Since both cars are parked, they are not moving. Therefore, the velocity of both cars is zero.
- Kinetic Energy (KE) = 0.5 * mass * velocity² = 0.5 * mass * 0² = 0.
- Thus, the kinetic energy of both cars is zero.
- Potential Energy (PE) is given by the formula: PE = mass * g * height, where g is the acceleration due to gravity (approximately 9.81 m/s²).
- For Car 1 (parked on the roadside):
- Height = 0 (ground level).
- PE1 = mass * g * 0 = 0.
- For Car 2 (parked on the second floor):
- Height = height of the second floor (let's assume it's a certain height, say h).
- PE2 = mass * g * h (where h > 0).
- Since Car 2 is at a height (h) above ground level, its potential energy (PE2) is greater than that of Car 1 (PE1 = 0).
- Therefore, PE2 > PE1.
- Since both cars have zero kinetic energy and Car 2 has greater potential energy than Car 1, we conclude that:
- The car on the second floor (Car 2) has more total energy than the car parked on the roadside (Car 1).
The car on the second floor of the building has more energy than the car parked on the roadside because it has greater potential energy due to its height.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A car traveled at 80 mph for the first half of the time of a trip and at 40 mph for the second half of the trip. What is the average speed of the car during the entire trip?
A20B40C50D60A motor powers a model car so that after starting from rest, the car travels s inches in t seconds, where s=16t√t . Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
A4√tB16√tC16√tD16t
The angle of depression of a car parked on the road from the top of the 150 m high tower is 30∘.Find the distance of the car from the tower
View SolutionIn a large housing complex, there are 15 small buildings and 22 large building. Each of the large buildings has 10 floors with 2 apartments on each floor. Each of the small buildings has 12 floors with 3 apartments on each floor. How many apartments are there in all.
View SolutionIn a system used for spraying cars, a car body is positively charged. Neutral droplets of paint are then attracted to the car because the positive car body induces a charge on the droplets of paint. Which diagram best shows the charge pattern?
View SolutionIn a high -rise building with 84 floors, one delivery boy delivers at every 6th floor and the other at every 8th floor. If the two start delivering together from the entrance of the building, at which floors will they meet again?
View SolutionA car is fitted with a convex side-view mirror of focal length 20 cm. A second car 2.8m behind the first car is overtaking the first car at a relative speed of 15 ms. The speed of the image of the second car as seen in the mrror of the first one is:
View SolutionShows the position-time graphs of three cars A,B and C On the basis of the graphs answer the follwing questions:
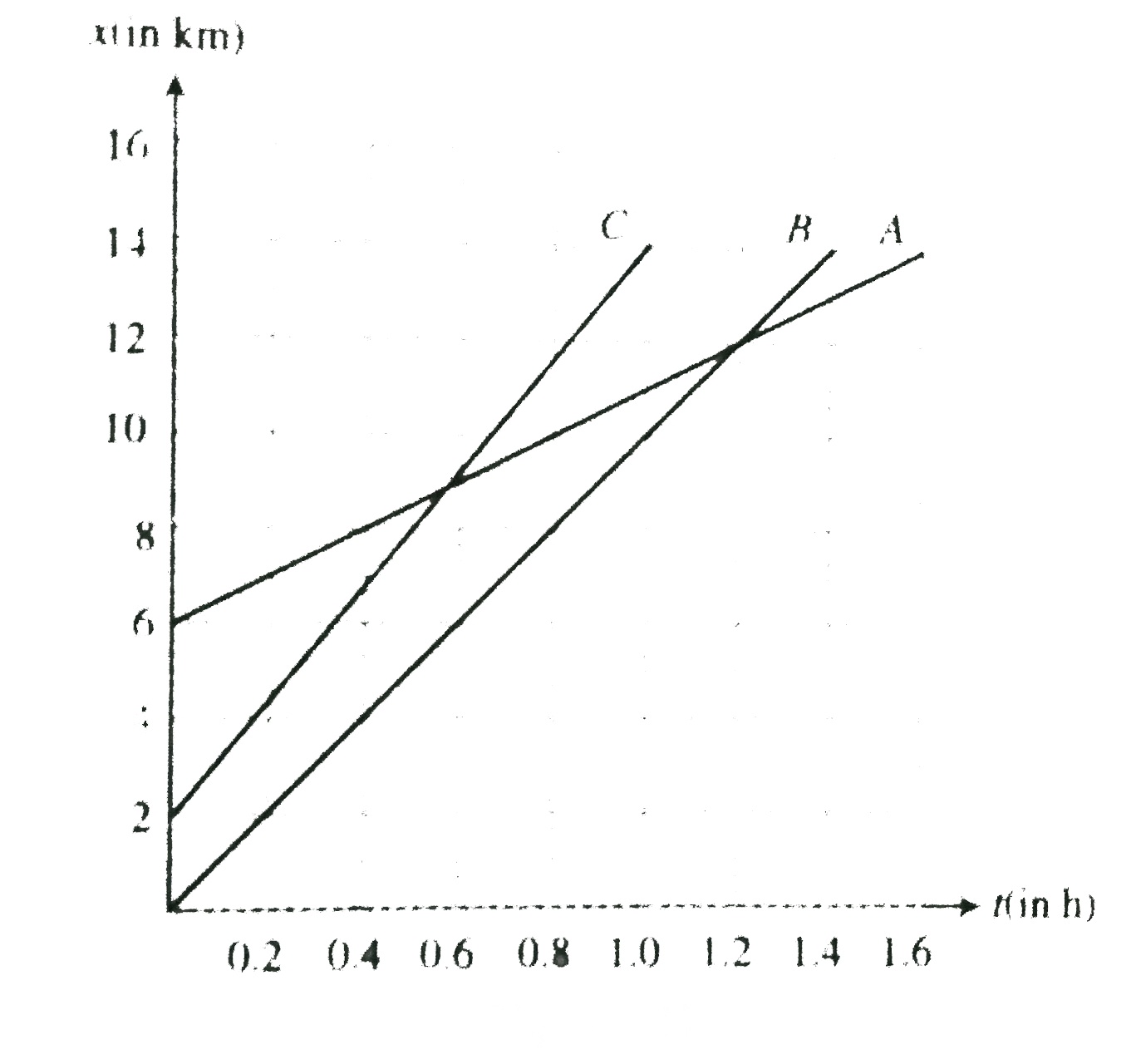 .
.
a. Which car has the highest speed and which the lowest?
b. Are the three cars evrs at the same point on the road?
c. When C passes A, wher is B?
d. What is the time interval during car A travel between the time it passed cars B and C ?.
e. What is the relative velocty of car B with respect to car C?
View Solution

