Two cars A and B are moving due east and due north at 60 km.p.h respetively. At noon A is west of B at a distance 40 km . When are the cars nearest to each other and what is the distance between them then ?

Text Solution

Verified by Experts

$A D_{1}$ represents the reversed velocity of B. $A B_{1}$ represents the velocity of A.AE represents the resultant of the two velocities which is the relative velocity of A with respect to B. The minimum distance between the two cars is BN. BN is perpendicular to AN.
The relative speed of $A = \sqrt{60^{\circ} + 80^{2}} = 100$ km.p.h
Let angle $B A N = θ$ . Let the two cars be nearest to each other after a time t .
$t = \frac{A N}{Relative speed} = \frac{A B cos θ}{100} = \frac{40}{100} \times \frac{60}{100} = \frac{6}{25} s$
The minimum distance between the two cars is BN.

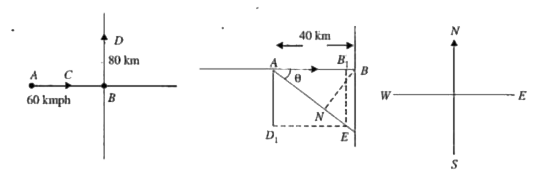
$B N = A B sin θ = 40 \times \frac{80}{100} = 32 k m$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two cars A and B are moving uniformly on two straight roads at right angles to one another at 40 and 20 km/h respectively. A passes the intersection of the road when B has still to move 50 km to reach it. The shortest distance between the two cars and the time when they are closet
A $20 \sqrt{} 5 k m ., 30 m$
B20 km., 10
C25 km., 20
Dnone of these
Question 2 - Select One
Two cars A and B are running in the same direction. Car ‘A’ had already covered a distance of 60 km. When car ‘B’ started running. The cars meet each other in 3 hours after car ‘B’ started running. What was the speed of Car ‘A’?
A40 kmph
B60 kmph
C45 kmph
DCannot be determined
Question 3 - Select One
A car moves with a speed of 40 km/h for 15 minutes and then with a speed of 60 km/h for the next 15 minutes. The total distance covered by the car is:
A100 km
B25 km
C15 km
D10 km

ICSE-VECTORS SCALARS ELEMENTARY CALCULUS -UNSOLVED PROBLEMS

Home
Ask Doubt
Profile