A body of mass 10 kg is at rest on an iinclined plane of angle 30∘ . What are its components parallel and perpendicular to the plane ?
The correct Answer is:(i) 49 N (ii) 84.9 N
To find the components of the gravitational force acting on a body of mass 10 kg resting on an inclined plane at an angle of 30 degrees, we can follow these steps:
Step 1: Identify the forces acting on the body
The only force acting on the body is the gravitational force (weight) which can be calculated using the formula:
Fg=mg
where:
- m=10kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
Step 2: Calculate the gravitational force
Substituting the values into the formula:
Fg=10kg×9.8m/s2=98N
Step 3: Resolve the gravitational force into components
The gravitational force can be resolved into two components:
1. Component parallel to the incline (F∥)
2. Component perpendicular to the incline ( F_{\perpendicular} )
Using trigonometric functions:
- The component parallel to the incline is given by:
F∥=mgsin(θ)
- The component perpendicular to the incline is given by:
F_{\perpendicular} = mg \cos(\theta)
Step 4: Calculate the parallel component
Substituting the values for θ=30∘:
F∥=98N×sin(30∘)
Since sin(30∘)=12:
F∥=98N×12=49N
Step 5: Calculate the perpendicular component
Now, calculate the perpendicular component:
F_{\perpendicular} = 98 \, \text{N} \times \cos(30^\circ)
Since cos(30∘)=√32:
F_{\perpendicular} = 98 \, \text{N} \times \frac{\sqrt{3}}{2}
Calculating this gives:
F_{\perpendicular} = 49 \sqrt{3} \, \text{N} \approx 84.87 \, \text{N}
Final Result
- The component of the gravitational force parallel to the incline is 49N.
- The component of the gravitational force perpendicular to the incline is approximately 84.87N.
The only force acting on the body is the gravitational force (weight) which can be calculated using the formula:
Fg=mg
where:
- m=10kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
Substituting the values into the formula:
Fg=10kg×9.8m/s2=98N
The gravitational force can be resolved into two components:
1. Component parallel to the incline (F∥)
2. Component perpendicular to the incline ( F_{\perpendicular} )
- The component parallel to the incline is given by:
F∥=mgsin(θ)
- The component perpendicular to the incline is given by:
F_{\perpendicular} = mg \cos(\theta)
Substituting the values for θ=30∘:
F∥=98N×sin(30∘)
Since sin(30∘)=12:
F∥=98N×12=49N
Now, calculate the perpendicular component:
F_{\perpendicular} = 98 \, \text{N} \times \cos(30^\circ)
Since cos(30∘)=√32:
F_{\perpendicular} = 98 \, \text{N} \times \frac{\sqrt{3}}{2}
Calculating this gives:
F_{\perpendicular} = 49 \sqrt{3} \, \text{N} \approx 84.87 \, \text{N}
- The component of the gravitational force parallel to the incline is 49N.
- The component of the gravitational force perpendicular to the incline is approximately 84.87N.
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - FROM SCALAR PRODUCT AND VECTOR PRODUCT
20 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - SELECTED PROBLEMS (FROM VECTOR ADDITION )
14 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound
10 Videos
Similar Questions
The plane parallel to YZ- plane is perpendicular to ………….
View SolutionA block of mass 2kg is pushed down an inclined plane of angle 37∘ above horizontal with a force parallel to inclined plane. The coefficient of friction is 3/4. The block moves 10m in 2 seconds starting form rest. The magnitude of the force is
View SolutionA mass of 2kg lies on a plane making an anged 300 to the horizontal. Resolve its weight along and perpendicular to the plane. Assume g=10ms−2.
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

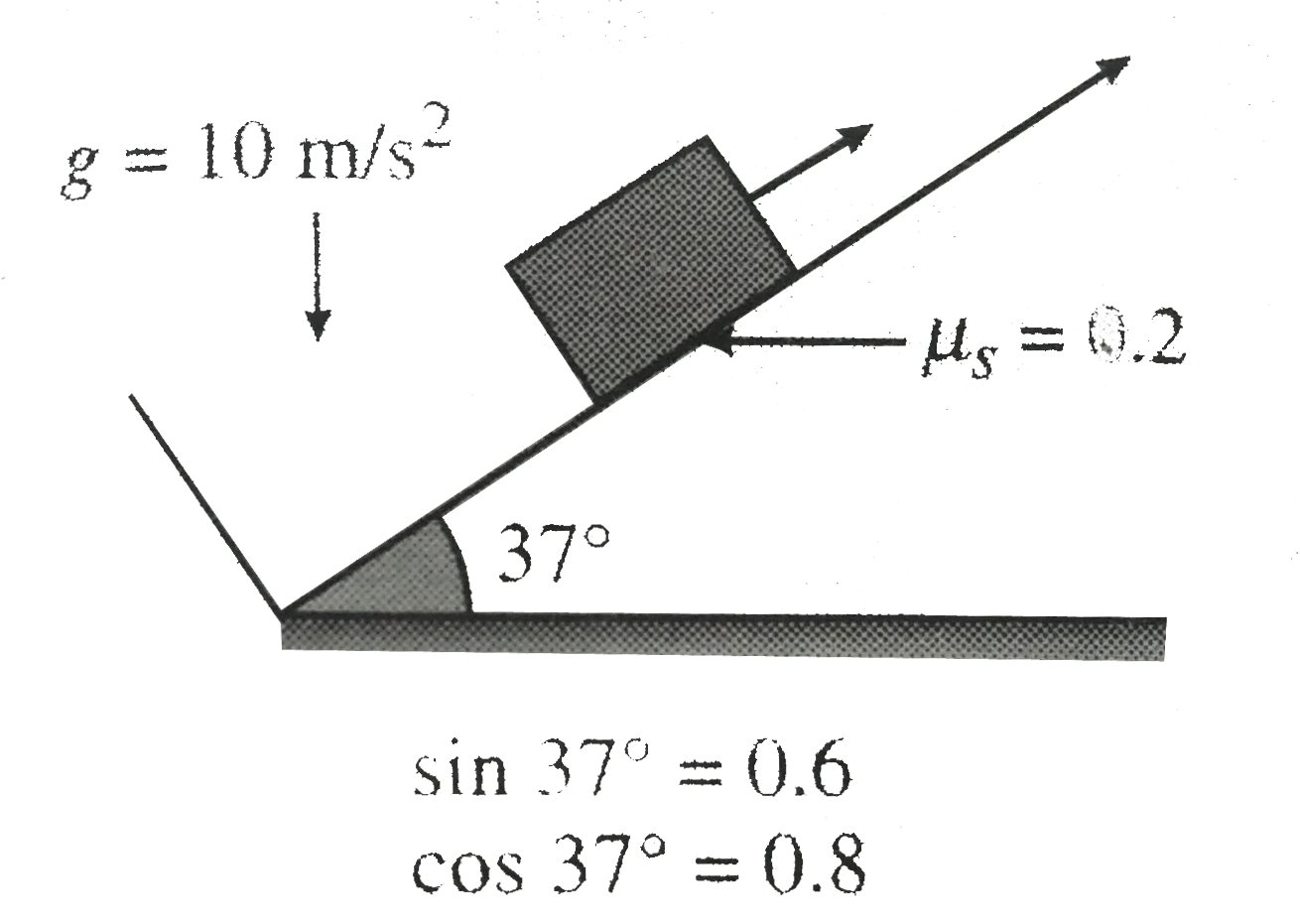
View SolutionAn object of mass 10kg is to be kept at rest on an inclined plane making an angle of 37∘to the horizontal by applying a force F along the plane upwards as shown in figure . The coefficient of static fiction between the object and the plane is 0.2 Find the magnitude of force F
[Take g=10ms−2]
View SolutionA force →F is applied to block (m=6kg) at rest on an inclined plane of inclination 30∘. The force →F is horizontal and parallel to surface of inclined plane. Maximum value of F so that block remains at rest is 40N. The coefficient of friction of the surface is.
View SolutionA partaicle of mass 1 kg and carrying 0.01 C is at rest on an inclined plane of angle of 30∘ with horizontal when an electric field of 490√3NC−1 applied parallel to horizontal, the coefficient of friction is
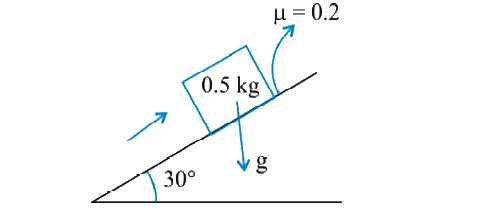
View SolutionA block of mass 0.5 kg is kept on a rough inclined plane making an angle of 30∘ with horizontal. What power will be required to move the block up the plane (along the plane) with a velocity of 5m/s ? (Take m = 0.2 between block and plane)
View SolutionA body of mass m=18kg is placed on an inclined plane the angle of inclination is α=37∘ and is attached to the top end of the slope with a thread which is parallel to the slope. Then the plane slope is moved with a horizontal acceleration of a. Friction is negligible.
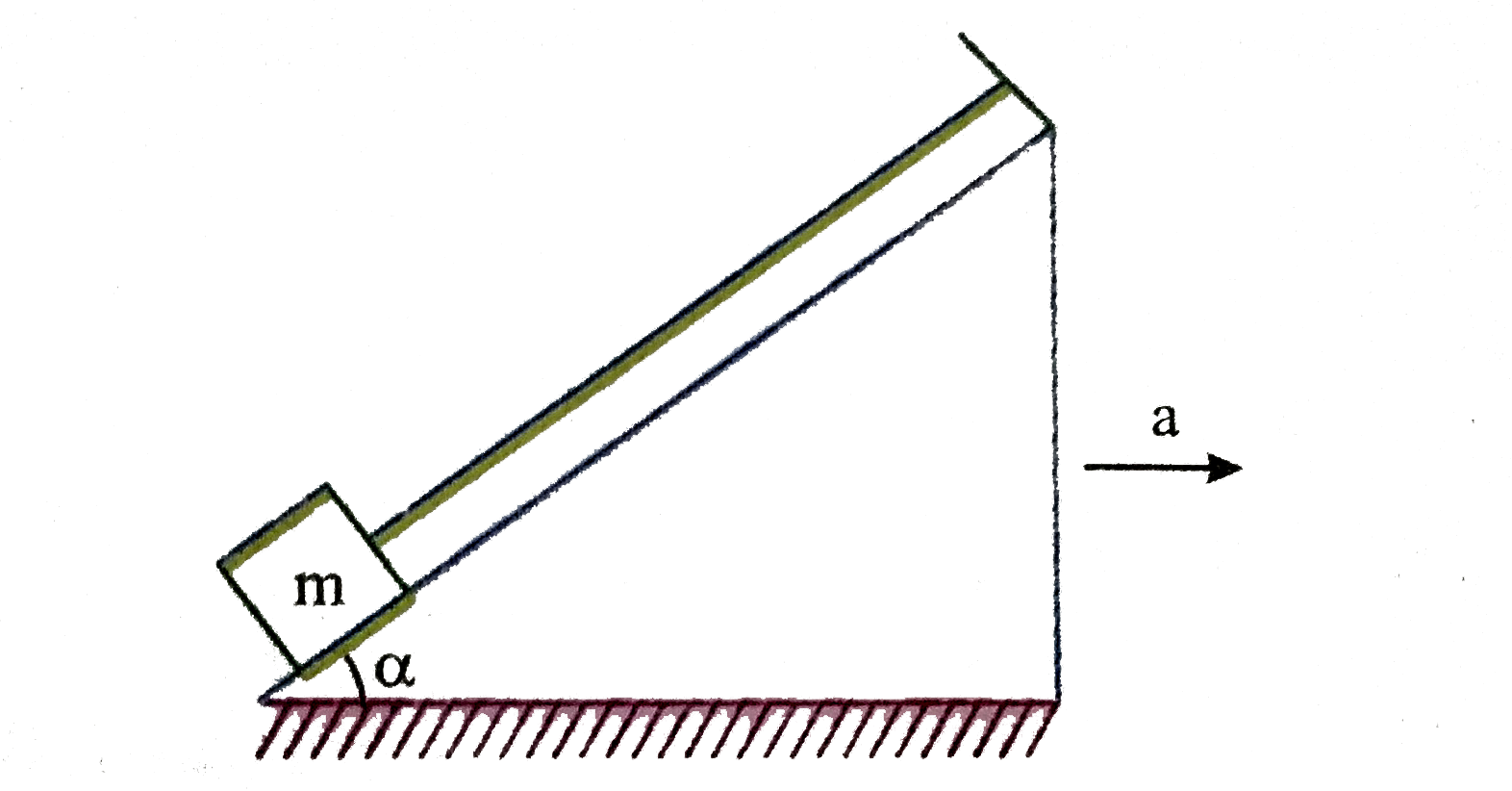
At what acceleration will the body lose contact with plane .
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View Solution
