A water-alcohol mixture is prepared such that its density is exactly equal to the density of some oil. What would be the shape of a drop of that oil in the given mixture and why?
To determine the shape of a drop of oil in a water-alcohol mixture where the density of the mixture is equal to the density of the oil, we can follow these steps:
Step 1: Understand the Concept of Density
Density is defined as mass per unit volume. When two substances have the same density, they exert equal buoyant forces on each other.
Step 2: Analyze the Situation
In this scenario, we have a drop of oil that is placed in a water-alcohol mixture. The density of the mixture is equal to the density of the oil.
Step 3: Consider the Forces Acting on the Drop
When the drop of oil is placed in the mixture, two main forces act on it:
- The gravitational force (weight) acting downwards.
- The buoyant force acting upwards, which is equal to the weight of the fluid displaced by the drop.
Step 4: Determine the Equilibrium Condition
Since the density of the oil and the density of the mixture are equal, the buoyant force acting on the oil drop will exactly balance the weight of the oil drop. This means that the drop will neither sink nor rise; it will remain suspended in the mixture.
Step 5: Analyze the Shape of the Drop
The shape of a liquid drop is influenced by surface tension. When a drop is in equilibrium (neither rising nor sinking), surface tension minimizes the surface area for a given volume. The shape that minimizes surface area is a sphere.
Conclusion
Therefore, the shape of the drop of oil in the water-alcohol mixture will be spherical because:
- The weight of the drop is balanced by the buoyant force.
- Surface tension acts to minimize the surface area, leading to a spherical shape.
Final Answer
The shape of the drop of oil in the given mixture will be spherical.
---
Density is defined as mass per unit volume. When two substances have the same density, they exert equal buoyant forces on each other.
In this scenario, we have a drop of oil that is placed in a water-alcohol mixture. The density of the mixture is equal to the density of the oil.
When the drop of oil is placed in the mixture, two main forces act on it:
- The gravitational force (weight) acting downwards.
- The buoyant force acting upwards, which is equal to the weight of the fluid displaced by the drop.
Since the density of the oil and the density of the mixture are equal, the buoyant force acting on the oil drop will exactly balance the weight of the oil drop. This means that the drop will neither sink nor rise; it will remain suspended in the mixture.
The shape of a liquid drop is influenced by surface tension. When a drop is in equilibrium (neither rising nor sinking), surface tension minimizes the surface area for a given volume. The shape that minimizes surface area is a sphere.
Therefore, the shape of the drop of oil in the water-alcohol mixture will be spherical because:
- The weight of the drop is balanced by the buoyant force.
- Surface tension acts to minimize the surface area, leading to a spherical shape.
The shape of the drop of oil in the given mixture will be spherical.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS) SELECTED PROBLEMS( FROM THE DEFINITION OF SURFACE TENSION)
27 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS) FROM CAPILLARY
15 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS)SHORT ANWER QUESTIONS
23 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
For the arrangement shown in the figure, what is the density of oil?
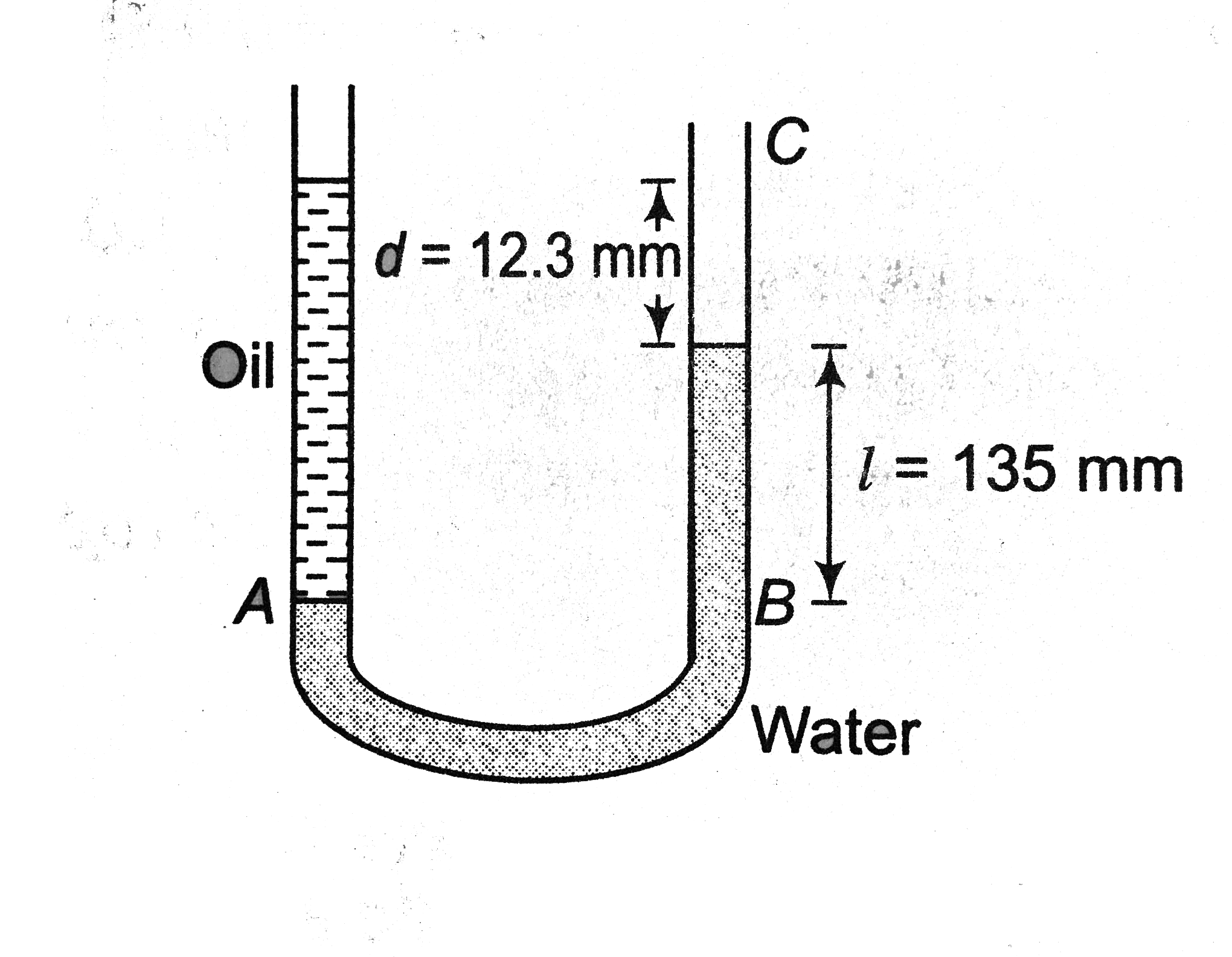 .
.
View SolutionFor the arrangement shown in the figure, what is the density of oil?
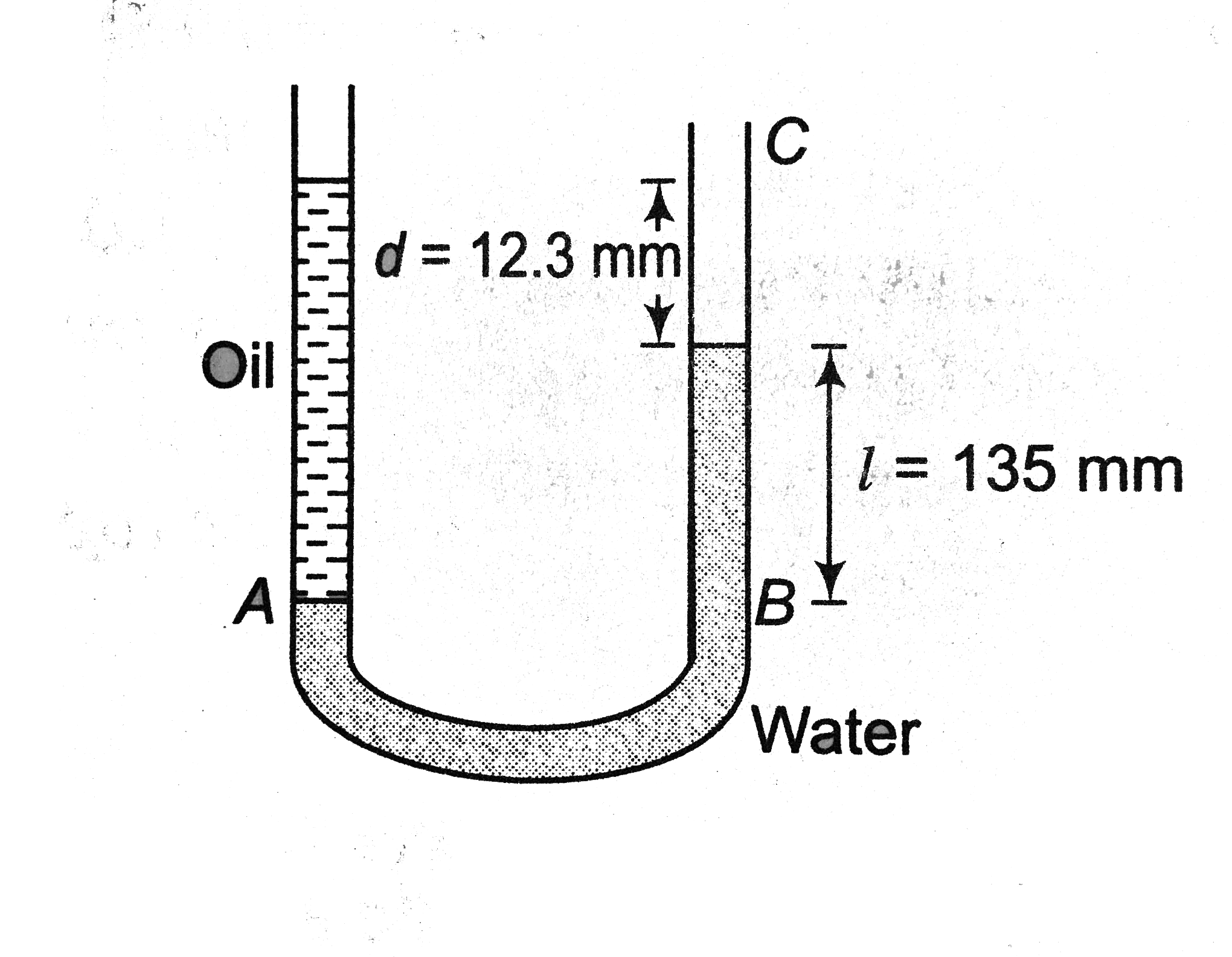 .
.
View SolutionAt what temperature the density of water is maximum? State its value.
View SolutionIs Oil in water is a heterogeneous mixture?
View SolutionA mixture of mustard oil and water forms
View SolutionA mixture of petrol and ethyl alcohol contains 22.0 % alcohol. The density of the mixture is 0.800gmL−1. What mass of alcohol is there in 40.0 mL of the mixture?
View SolutionA liquid mixture of volume V, has two liquids as its ingredients with densities α and β. If density of the mixture is σ, then mass of the first liquid in mixture is
View SolutionA mixture of NO2 and N2O4 has a vapour density of 38.3 at 300K. What is the number of moles of NO2 in 60g of the mixture?
View SolutionA mixture of NO2 and N2O4 has a vapour density of 38.3 at 300K. What is the number of moles of NO2 in 90g of the mixture?
View SolutionA mixture of NO2 and N2O4 has a vapour density of 38.3 at 300K. What is the number of moles of NO2 in 80g of the mixture?
View Solution
