Calculate the radius of the capillary tube if, when it is dipped vertially into a beaker of water, the water stands 35 cm higher in capillary tube than in the beaker. Surface of water is 0.073Nm−1.
The correct Answer is:4.3×10−5m
To calculate the radius of the capillary tube, we can use the formula that relates the height of the liquid column in the capillary tube to the surface tension, density, and gravitational acceleration. The formula is given by:
h=2σρgr
Where:
- h = height of the liquid column (in meters)
- σ = surface tension of the liquid (in N/m)
- ρ = density of the liquid (in kg/m³)
- g = acceleration due to gravity (in m/s²)
- r = radius of the capillary tube (in meters)
Step 1: Convert the height from cm to meters
Given that the height h is 35 cm, we convert it to meters:
h=35cm=0.35m
Step 2: Identify the known values
- Surface tension σ=0.073N/m
- Density of water ρ=1000kg/m3
- Acceleration due to gravity g=9.8m/s2
Step 3: Rearrange the formula to solve for the radius r
Rearranging the formula to isolate r:
r=2σρgh
Step 4: Substitute the known values into the formula
Substituting the known values into the rearranged formula:
r=2×0.0731000×9.8×0.35
Step 5: Calculate the value of r
Calculating the numerator:
2×0.073=0.146
Calculating the denominator:
1000×9.8×0.35=3430
Now, substituting these values into the equation for r:
r=0.1463430≈4.26×10−5m
Step 6: Final answer
Thus, the radius of the capillary tube is approximately:
r≈4.3×10−5m
- h = height of the liquid column (in meters)
- σ = surface tension of the liquid (in N/m)
- ρ = density of the liquid (in kg/m³)
- g = acceleration due to gravity (in m/s²)
- r = radius of the capillary tube (in meters)
Given that the height h is 35 cm, we convert it to meters:
h=35cm=0.35m
- Surface tension σ=0.073N/m
- Density of water ρ=1000kg/m3
- Acceleration due to gravity g=9.8m/s2
Rearranging the formula to isolate r:
r=2σρgh
Substituting the known values into the rearranged formula:
r=2×0.0731000×9.8×0.35
Calculating the numerator:
2×0.073=0.146
1000×9.8×0.35=3430
r=0.1463430≈4.26×10−5m
Thus, the radius of the capillary tube is approximately:
r≈4.3×10−5m
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (KINETIC THEORY OF GASES ) CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
5 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (KINETIC THEORY OF GASES ) LONG ANSWER QUESTIONS
9 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS) SELECTED PROBLEMS( FROM THE DEFINITION OF SURFACE TENSION)
27 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
A uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
View SolutionThe lower end of a capillary tube is dipped into water and it is seen that the water rises through 7.5 cm in the capillary. Find the radius of the capilary. Surface tension of water =7.5×10−2Nm−1. Contact angle between water and glass =0∘.Takeg=10ms−2.
View SolutionIf a wax coated capillary tube is dipped in water, then water in it will-
View SolutionWater rises to height h in capillary tube. If the length of capillary tube above the surface of water is made less than h then
View SolutionCalculate the difference h in water levels in two commnicating capillary tube of radius 1mm and 1.5mm. Surface tension of water=0.07Nm−1

View SolutionTwo capillary tubes P and Q are dipped in water. The height of water level in capillary P is 2/3 to the height in Q capillary. The ratio of their diameters is
View SolutionA glass tube of radius 0.4mm is dipped vertically in water. Find upto what height the water will rise in the capillary? If the tube in inclined at an angle of 60∘ with the vertical, how much length of the capillary is occupied by water? Suface of water=7.0×10−2N/m,density of water =103kg/m3.
View SolutionIn a capillary tube of radius 'R' a straight thin metal wire of radius 'r' (R>r) is inserted symmetrically and one of the combination is dipped vertically in water such that the lower end of the combination Is at same level . The rise of water in the capillary tube is [T=surface tensiono of water ρ =density of water ,g =gravitational acceleration ]
View SolutionWater rises in a capillary tube to a height 4 cm. If the tube is inclined at an angle of 45∘ with the vertical , find the position of the water in the tube.
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
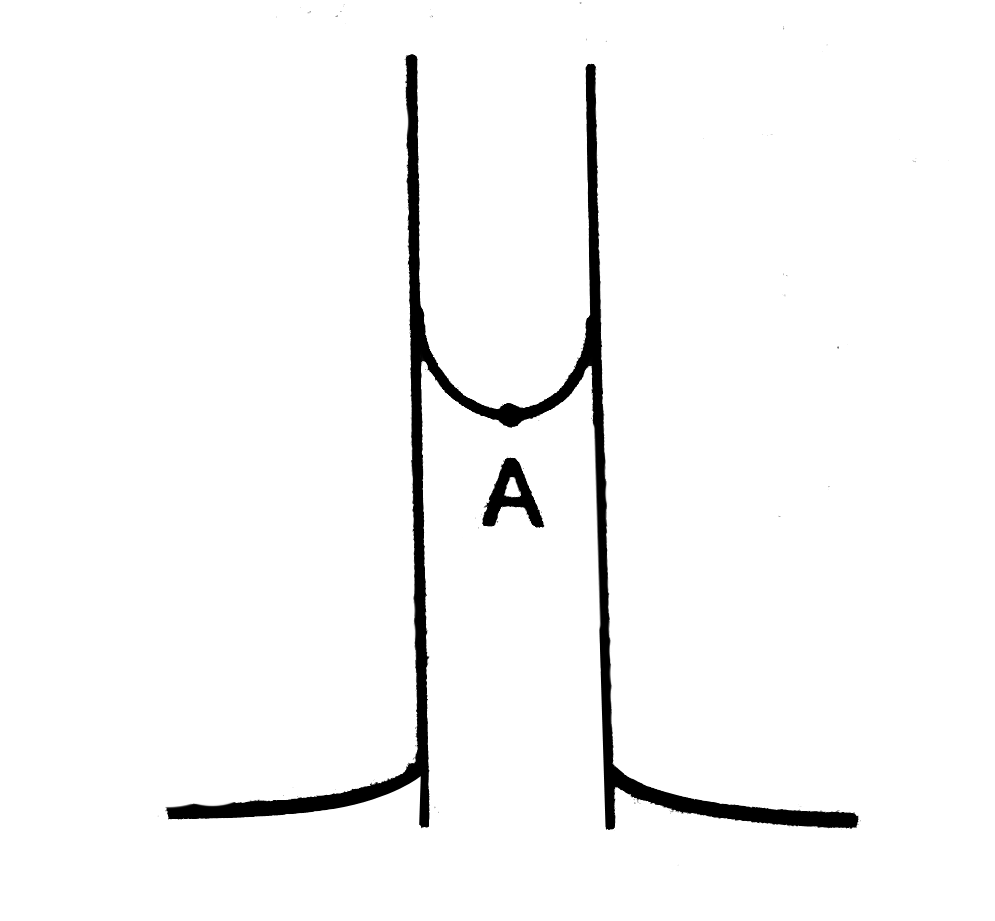
View Solution
