If the gravitational force had varied as r−5/2 instead of r−2 the potential energy of a particle at a distance 'r' from the centre of the earth would be proportional to
r−1
r−2
r−3/2
r−5/2
The correct Answer is:C
To find the potential energy of a particle at a distance 'r' from the center of the Earth when the gravitational force varies as r−5/2, we can follow these steps:
Step 1: Understand the relationship between force and potential energy
The potential energy U(r) for a conservative force can be found by integrating the force from infinity to a distance r:
U(r)=−∫r∞Fdr
Step 2: Define the gravitational force
The gravitational force F is given as:
F=Gm1m2r5/2
where G is the gravitational constant, and m1 and m2 are the masses involved.
Step 3: Set up the integral for potential energy
Substituting the expression for F into the potential energy equation, we have:
U(r)=−∫r∞Gm1m2r5/2dr
Step 4: Perform the integration
To integrate 1r5/2, we can rewrite it as:
U(r)=−Gm1m2∫r∞r−5/2dr
The integral of r−5/2 is:
∫r−5/2dr=−23r−3/2
Thus, we have:
U(r)=−Gm1m2(−23r−3/2)r∞
Step 5: Evaluate the limits of the integral
Evaluating the limits, we find:
U(r)=−Gm1m2(−23r−3/2−0)=23Gm1m2r3/2
Step 6: Write the final expression
Thus, the potential energy U(r) is proportional to:
U(r)∝1r3/2
Conclusion
The potential energy of a particle at a distance r from the center of the Earth, when the gravitational force varies as r−5/2, is proportional to r−3/2.
---
The potential energy U(r) for a conservative force can be found by integrating the force from infinity to a distance r:
U(r)=−∫r∞Fdr
The gravitational force F is given as:
F=Gm1m2r5/2
where G is the gravitational constant, and m1 and m2 are the masses involved.
Substituting the expression for F into the potential energy equation, we have:
U(r)=−∫r∞Gm1m2r5/2dr
To integrate 1r5/2, we can rewrite it as:
U(r)=−Gm1m2∫r∞r−5/2dr
The integral of r−5/2 is:
∫r−5/2dr=−23r−3/2
Thus, we have:
U(r)=−Gm1m2(−23r−3/2)r∞
Evaluating the limits, we find:
U(r)=−Gm1m2(−23r−3/2−0)=23Gm1m2r3/2
Thus, the potential energy U(r) is proportional to:
U(r)∝1r3/2
The potential energy of a particle at a distance r from the center of the Earth, when the gravitational force varies as r−5/2, is proportional to r−3/2.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (ELASTICITY )
22 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (SURFACE TENSION )
23 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION (ROTATIONAL MOTION AND MOMENT OF INERTIA )
25 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
The field due to a magnet at a distance R~ from the centre of the magnet is proportional
View SolutionThe gravitational potential energy of a body at a distance r from the center of the earth is U. The force at that point is :
View SolutionCalculate the gravitational potential energy of a body of mass 100 kg at a distance of 6 km from the centre of the earth.
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionA sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
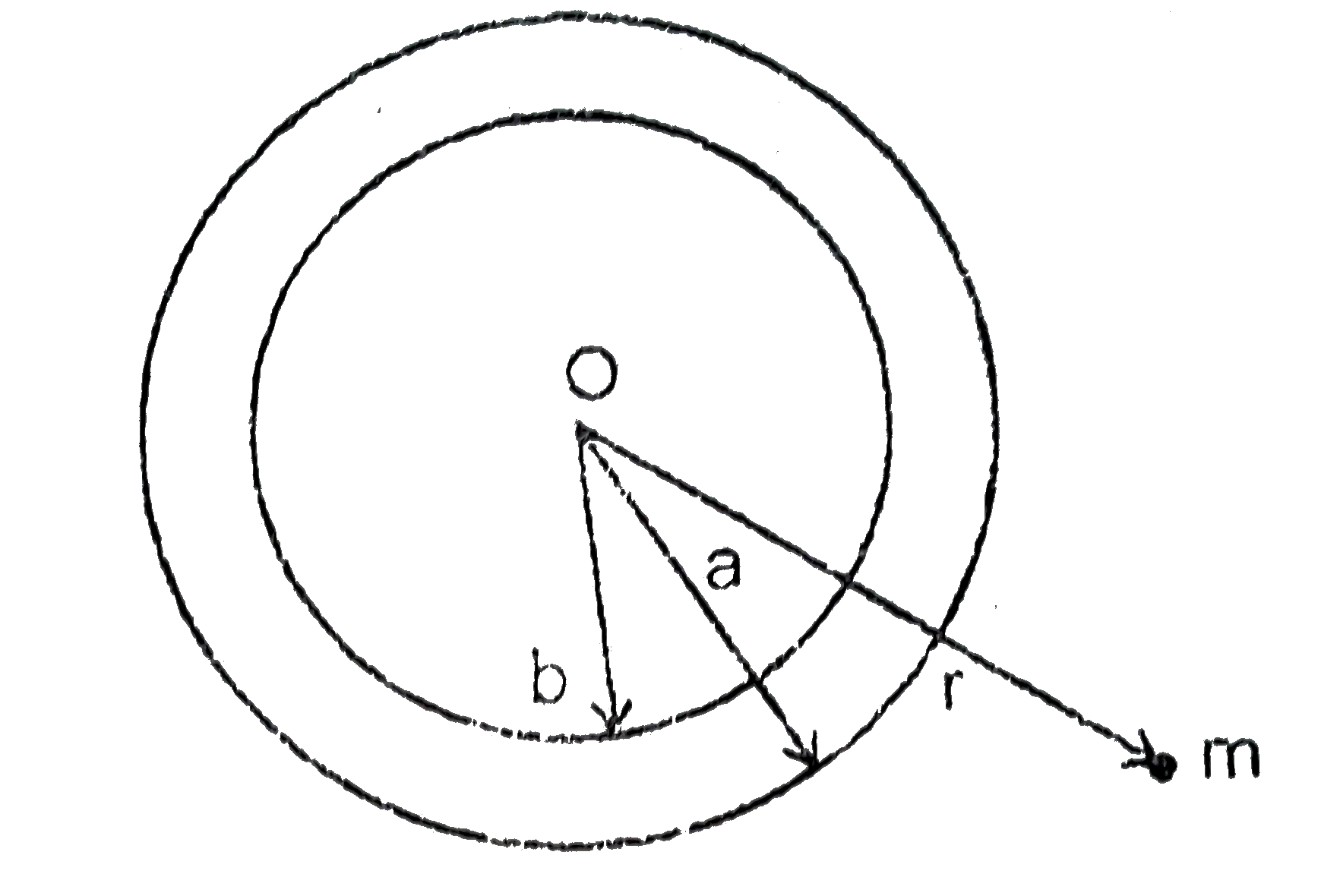 ,
,
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
View SolutionSuppose the gravitational force varies inversely as the nthpower of distance. Then the time period of a planet in circular orbit of radius R around the sun will be proportional to-
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionIf Me is the mass of earth and Mm is the mass of moon (Me=81Mm). The potential energy of an object of mass m situated at a distance R from the centre of earth and r from the centre of moon, will be :-
View Solution
